因数分解の公式が使えない問題1 問題1 x 3 +x 2 y-x-y 「共通因数をくくり出す」はできません。 「因数分解の公式を使う」もだめですね。 よって、「最低次数の文字について整理する」です。 この問題の場合、xは3次、yは1次ですから、yについて整理します。 yを含む項とyを含まない項にグループ分けします。 (x 2 y-y)+(x 3 -x) ( )の中の 高校の数学では,最初に「数と式」という分野を学習します(数学 i )。ここでは、単項式や多項式、それに整式、式の展開公式などを学びますが、その次に待ち受けているのが「因数分解」です。因数分解は、数学 i だけでなく今後の数学でずっと登場する重要な内容です。因数分解しなさい ①4a 2bc12ab 2c8abc 2 ②2x 25x3 ③49x 216y 2z 2 ④6x 27x3 ⑤8x 2y10xy3y ⑥x 3x ⑦x 39x 2x ⑧3ax 218ax27a ⑨ (x2) 25 (x2) ⑩ (x3) 2 (x3)12 ⑪ (2ab) 2 (a2b) 2 ⑫x 26xy9y 225 ⑬x 210x25y 2 ⑭x 22xyy 29 1⑧の解説 2の解説 解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。 解説リクエスト 解説リクエストフォーム 問題
中3数学12 式の計算6 因数分解 基本問題プリント 問題 306
数学 因数分解 問題
数学 因数分解 問題-== 因数分解の入試問題 == 引用元の問題は記述式の問題ですが,以下の問題ではWeb画面上での操作性をよくするため,選択問題に変えています. まぐれ当たりでは力が付きませんので,計算用紙を使って,よく考えてから選択肢の内の1つをクリックしてください.解答すれば解説が出ます. 因数分解の公式 たしかめ3(p27) 問8(p27)問9(p27) 問10(p27) 問11(p28) 基本の問題1(p28) 2(p28) 中学3年数学 東京書籍1章2節 1因数分解 いろいろな式の因数分解 基本の問題 解説 解答 赤城花太朗




高校数学 数 10 因数分解 応用編 Youtube
Try IT(トライイット)のたすきがけを使う因数分解の練習の映像授業ページです。 Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。高校講座HOME >> 数学Ⅰ >> 第3回 数と式 因数分解 数学Ⅰ Eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。 出演者紹介 今回は工夫が必要な因数分解を見ていこう。なお、難関レベルの問題も少し扱う。 中学生レベルだと難問かもしれないが、高校生以上なら基本問題だと思う。 前回 因数分解の基本と練習問題(2)(標) 次回 因数分解の工夫(2)(標~難)
式の計算因数分解(たすき掛け) s 練習問題 3次の式を因数分解せよ。 D E D F D E因数分解(基本問題2) 次の式を因数分解しなさい ax 23a 12a 3 4a 4ax 2 6a x 2 7x12 x 2 15x56 x 2 6x9 次の式を因数分解しなさい x 2 11x30 x 212x x 23x2 x 216x64 x 21 x 2y 2 次の式を因数分解しなさい x 2 4x5 x 23x4 x 2x6 x 22x8 x 24x12 x 2 24x144 問題 整数係数の範囲で次の因数分解をする。 ① $x^44y^4$ ② $x^5x^41$ ③ $(ab)(bc)(ca)abc$ ④ $x^52x^43x^33x^22x1$ ⑤ $x^86x^63x^42x^29$ ⑥ $(xy)^3(yz)^3(zx)^3$ 解答 1番 $x^44y^4=x^44x^2y^24y^44x^2y^2=(x^22y^2)^2(2xy)^2$ $=(x^22xy2y^2)(x^22xy2y^2)$ 2番
高校の数学Ⅱで扱う因数分解の基本から応用までの練習問題です。 因数分解は展開の逆演算です。 展開は乗法公式を覚えていなくても必ずできますが、因数分解は基本公式を覚えていないとできません。 応用となると少し手を加えないと先因数分解公式① 共通因数をくくりだす。 因数分解公式② 掛けて足して 因数分解公式③④ 二乗になる 因数分解の公式⑤ 二乗ひく二乗 因数分解の公式中学生まとめ! 数学の成績が落ちてきたと焦っていませんか? こちらの関連記事はいかが中学3年生 数学 式の活用 問題プリント 無料ダウンロード・印刷 乗法公式や因数分解の公式を使って式を簡単に解く方法や具体的な場面で活用する練習ができる問題プリントを無料ダウンロード・印




高校数学 数 10 因数分解 応用編 Youtube




高校入試 因数分解の難問を解説 難関高校の入試問題に挑戦しよう 数スタ
因数分解の応用 2つに分けて共通因数から考える因数分解や、因数分解を2段階行うなどの応用問題について学習します。 ( )でまとめる因数分解 分けて解く因数分解 因数分解の応用 因数分解の応用 因数分解の応用 因数分解の応用 因数分解の応用因数分解とは 因数分解とは、 展開の逆 であり 積の形をつくること です。 例えば、 \(x^2x6=(x2)(x3)\) という風に、1つの整式(和や差の形)を積の形に表します。 この積をつくっている各式を、もとの式の因数といいます。 高校の因数分解を5分でマスター! 現役塾講師によるラクラク数学講座 はぁ、因数分解がなんとなく苦手です。 簡単な問題なら解けるけど、応用問題や3次式の問題になると、とたんに解けなくなる。 もう一度 基礎から学んで、「たすき掛け」や




数学 質問解答 因数分解の難問 共通因数をくくる問題 中学数学 中3 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生
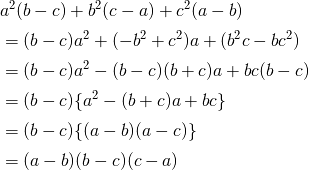



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局
中学数学 因数分解 練習問題集 基礎力養成 数学練習問題集シリーズ Kindle版 中学数学 因数分解 練習問題集 基礎力養成 数学練習問題集シリーズ Kindle版 山本ごん太 (著) 形式 Kindle版 5つ星のうち45 4個の評価 その他 の形式およびエディションを表示するまずこの動画を見る際に、前提として知っておいてほしいのが、 展開と因数分解は逆の計算手順 だということです。 (2x+5) (3x+4)というのは、 (2x+5)のかたまり掛ける (3x+4)のかたまり、というように掛け算でつながった状態になっていますね。 このように、 掛け算でつながった状態 のことを 因数分解されたかたち だと思っておいてください。 最初に展開の話中学校数学科 第3学年 1 式の展開と因数分解 知識・技能の習得を図る問題 中学校 年 組 号 氏名 第3学年 1 式の展開と因数分解 b b blb1 x Î 0 Éwbèb b bl ( # $å ²bé




中学数学 因数分解 練習問題集 基礎力養成 数学練習問題集シリーズ 山本権太 数学 Kindleストア Amazon



中3数学12 式の計算6 因数分解 基本問題プリント 問題 306
1つの文字で整理する因数分解: 説明 ・ 例題 ・ 練習問題 対称式・交代式の因数分解: 説明 ・ 例題 ・ 練習問題 複2次式の因数分解: 説明 ・ 例題 ・ 練習問題 公式を利用した高次方程式の因数分解: 説明 ・ 例題 ・ 練習問題 3乗の基本公式を利用した因数分解(基本問題1) 次の式を因数分解しなさい x 2 4x 4x 22x axay x 2 3x2 x 2 6x5 x 2 12x 次の式を因数分解しなさい x 2 7x10 x 2 11x10 x 211x30 x 213x42 x 26x9 次の式を因数分解しなさい x 2 2x35 x 2 x30 x 2 3x40 x 2 18x81 x 29 x 216 3:たすき掛けで因数分解してみよう!(練習問題) では早速、問題を解いてみましょう。たすき掛けを習得するにはなるべく多くの問題を解くことが鍵です! 練習問題1 x 2 4x3 をたすき掛けを使って因数分解せよ。 解答&解説 x 2 の係数は1、定数項は3です。




中学数学 多項式 の教え方 因数分解




中学3年数学 因数分解 因数分解をわかりやすく解説 高校入試出題率100 数学の面白いこと 役に立つことをまとめたサイト
の因数分解を、混ざった問題でやると、詰まる。 また、このレベルでは、足して〇〇掛けて〇〇の方法ですべてを解こうとする。 テスト直前で時間がない場合、足して〇〇掛けて〇〇のやり方1本に統一して、 は捨てるか、特殊パターンで教えた方がいいかもしれない。 整数問題〜因数分解を使う問題〜 この記事では 整数 問題の中で 因数分解 を使うタイプの問題について解説していきます。 入試数学の整数問題を解く時の定石は以上の三種類があります。 主にいずれかに帰着させて問題を解くため、どのタイプを使えば 基本から発展問題まで 中学数学 因数分解! 基本から発展問題まで 因数分解は公式を使うだけですぐに解けるものもあれば、公式を使わないもの、解くまでにくふうが必要なものもあったりします。 展開より因数分解の方が難しい、と感じている人も多いようです。 そんな因数分解の共通因数や公式を使った基本問題から、文字の置き換えやくふうが必要



因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方




二次方程式で解の公式を使う問題 見分け方は因数分解がポイント 中学や高校の数学の計算問題
因数分解の難問|高校入試編・中学数学 にゃんこ 以下の式を因数分解せよ。 x 2 y − x y − 156 y x 2 y − x y − 156 y 解説(西大和学園高校) 中学数学の因数分解の基本を使って解く問題ですが、定数部分が多い場合の対処法を学べる良問です。 積が-156になり和が-1になる数値の組み合わせは、まず156を素因数分解してから、そのかたちを見ながら考えます。 和足して11、掛けて24になる数字(因数)を見つけ出し、分解するのです。 『因数に分解する』という考え方が将来役に立つ さて、この因数分解が将来何の役に立つのでしょうか。 それはこの問題の解き方ではなく、「因数に分解する」という考え方なの 数学Ⅰ目次 高校1年 数学I 因数分解予習用練習問題 ♡赤城( ᴗ ) ♡ ホーム ピグ アメブロ 芸能人ブログ 人気ブログ Ameba新規登録(無料)




中学数学 因数分解の解き方と練習問題 Irohabook




因数分解難問と意外な別解 怜悧玲瓏 高校数学を天空から俯瞰する
工夫して計算しよう。 2 (1)172 -132 の計算をする。 〈考え方〉 展開や因数分解をつかう。 172 -132 =(17+13)(17-13) =30×4 = 1 ・今までに学習してきたことを振り返り,乗法の公式の中に似たような形の式があるかどうかを4つの公式カードの中




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ




中学3年生 数学 計算たしかめミックス 練習問題 式の展開と因数分解 平方根 2次方程式 ちびむすドリル 中学生




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ
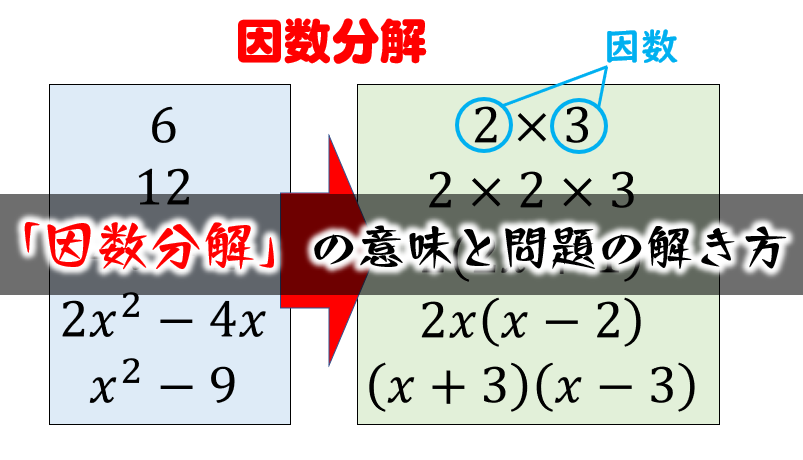



因数分解の意味 問題の解き方 数学fun




因数定理を利用した因数分解の練習問題 高校数学の知識庫
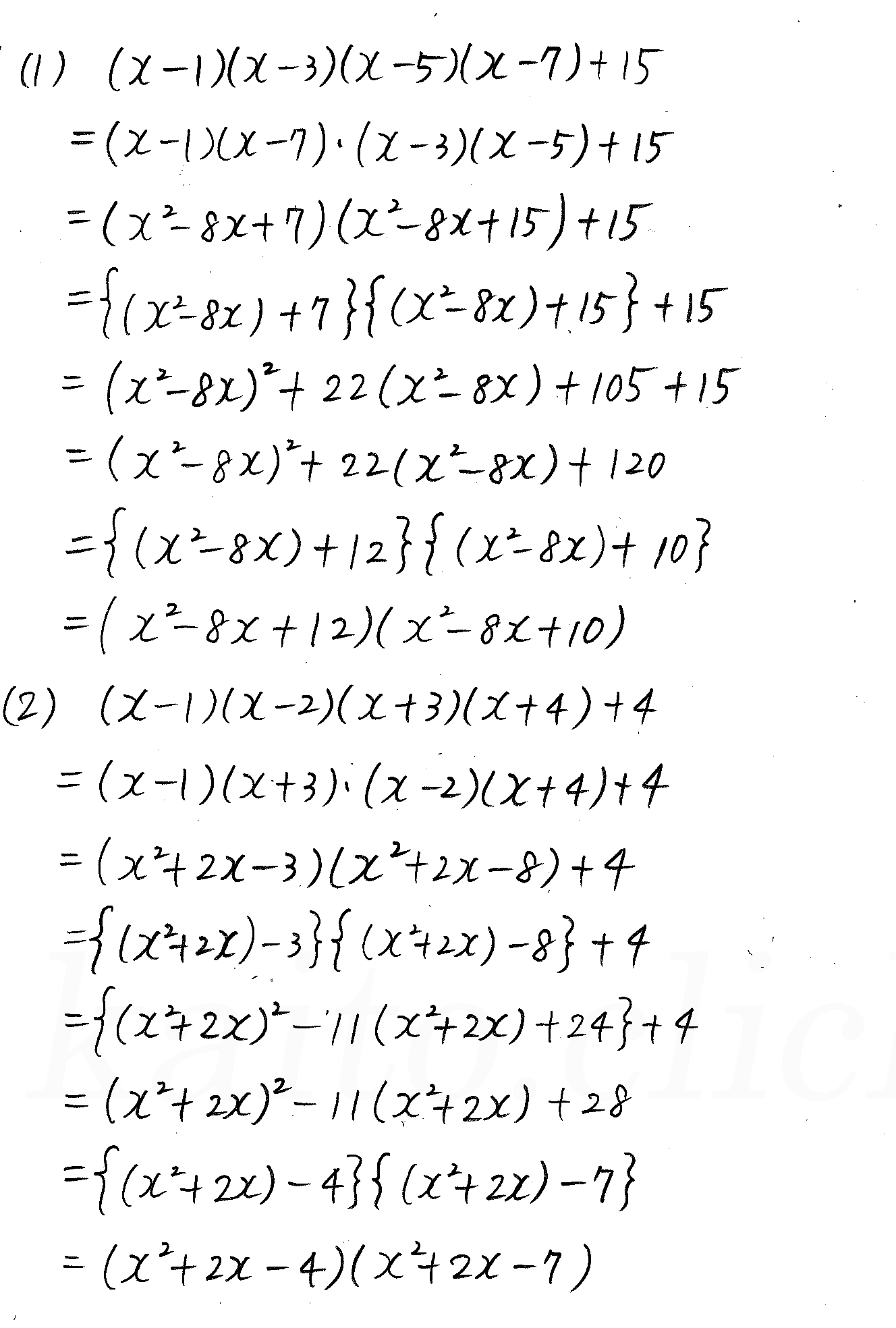



改訂版 3trial数学 P14 3 因数分解 練習問題




数学 中3 9 因数分解 もっと応用編 Youtube




高校数学 14 10 21講義4 因数分解 中学数学 高校数学




無料 中3数学 基本問題 問題プリント 304 式の計算4 素因数分解




中学数学 因数分解の解き方と練習問題 Irohabook




いろいろな因数分解 置き換え問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




無料 中3数学 標準問題 問題プリント 306 式の計算6 因数分解2




面白い因数分解 数学天才問題 う山先生の因数分解1問目 2018年4月12日 中学受験 算数プロ家庭教師 算数合格トラの巻 エキサイト ブログ




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解
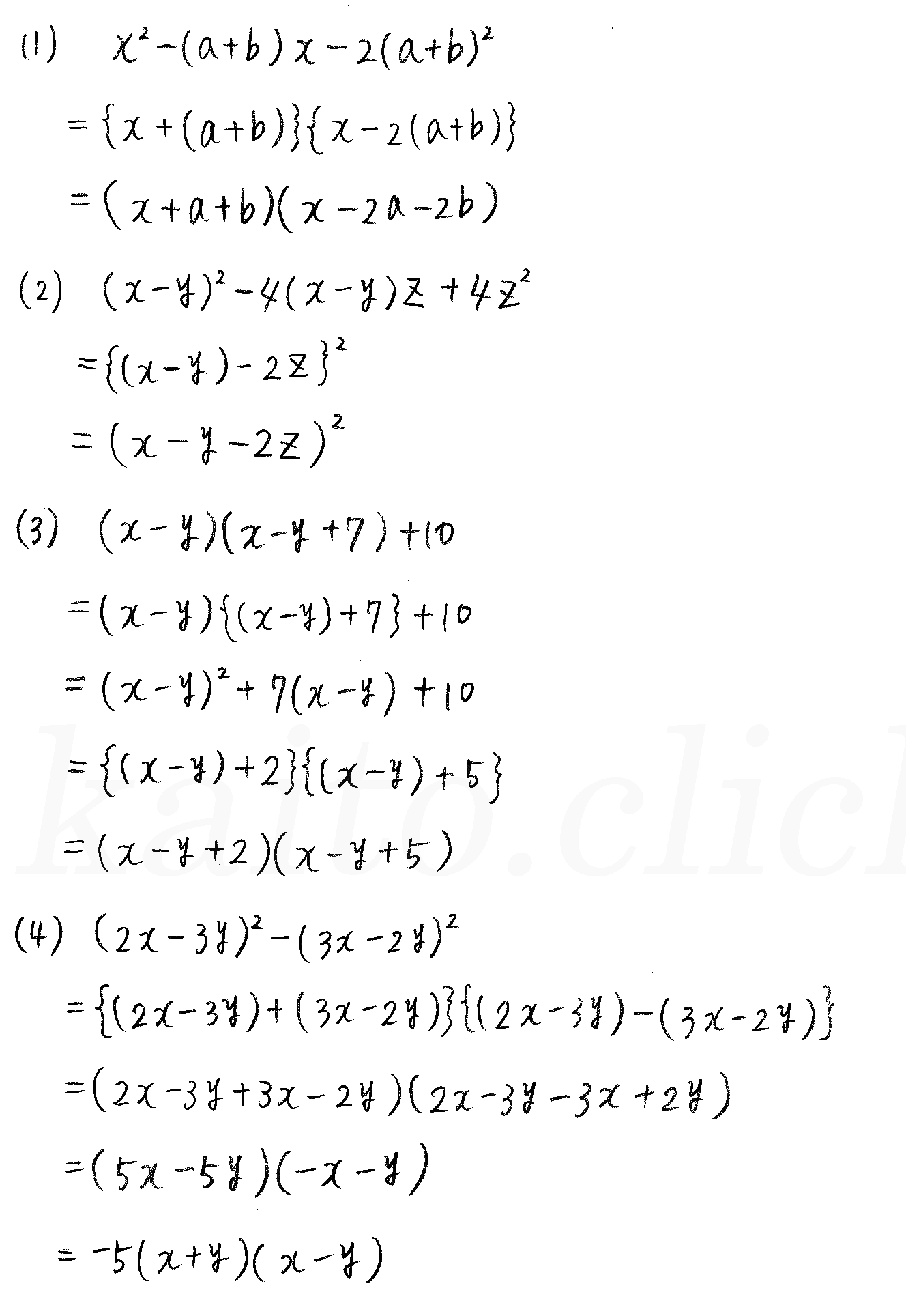



改訂版 クリアー数学 P15 5 因数分解 2




因数分解 おいしい数学



3




因数分解 スタディーx




中3 数学 因数分解7 因数分解の応用1 5分 Youtube




ちょっと難しい因数分解の問題 制限3分 中学数学 理科 寺子屋塾の復習サイト




数学 問題演習 たすき掛けを用いる因数分解 教科書より詳しい高校数学




数と方程式 3 難しい因数分解 交代式 数i A 東大数学9割のkatsuyaが販売する高校数学の問題集




数学実況 13 因数分解 中学生には難問 自作問題 Youtube



3




展開 因数分解の利用 図形 清水塾




中3 数学 1学期期末テスト いろいろな因数分解 赤城 ᐡᐤᐡ




高校入試 因数分解の難問を解説 難関高校の入試問題に挑戦しよう 数スタ




因数分解 これが解けたらすごいよ 苦手な数学を簡単に




間違いやすい因数分解 数学の基礎問題ですが 2割の大人は間違う因数分解 暇つぶしに動画で脳トレ



中3数学 二次方程式の解き方と因数分解 解の公式の覚え方と簡単な計算問題 猫に数学




因数定理を利用した因数分解の練習問題 高校数学の知識庫



高校数学因数分解 この問題がわかる方教えてください Yahoo 知恵袋




中3 中3数学 いろいろな因数分解 中学生 数学のノート Clear




無料 中3数学 発展 応用問題 問題プリント 305 式の計算5 因数分解1




その勉強 将来役に立つんです 数学 因数分解 編 スタディサプリ中学講座




高校入試 因数分解の難問を解説 難関高校の入試問題に挑戦しよう 数スタ



高校数学1の因数分解の応用編の問題なのですが 下の写真の 2 と 3 の Yahoo 知恵袋



中学3年生の数学問題アプリ はんぷく因数分解 タブガク




高校入試 難関校の因数分解を解説 Youtube



数と式の問題 Of 京極一樹の数学塾会員頁




因数分解のくくりだし 共通因数を見つける練習をしよう 中学や高校の数学の計算問題




公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ



Studydoctor x a x b の因数分解 中3数学 Studydoctor



まとめすぎた高校入試の因数分解難問 難関私立の問題 猫に数学




因数分解のいろいろな計算 無料で使える中学学習プリント



U9j580gf8iba369ji2w Xyz P 614
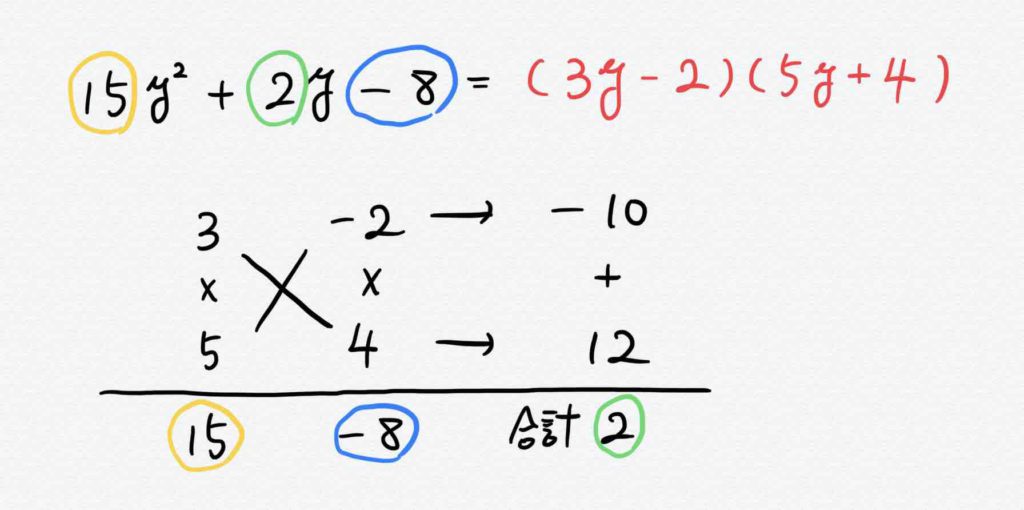



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局




高校数学 因数分解 練習問題集 基礎力養成 数学練習問題集シリーズ 山本権太 数学 Kindleストア Amazon




中3数学 因数分解とは 練習編 映像授業のtry It トライイット



3




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




高校数学 因数分解 解の公式を使ってルートが登場する因数分解を解けるようになろう 数学の面白いこと 役に立つことをまとめたサイト




中学3年の数学 動画 因数分解 の問題 19ch
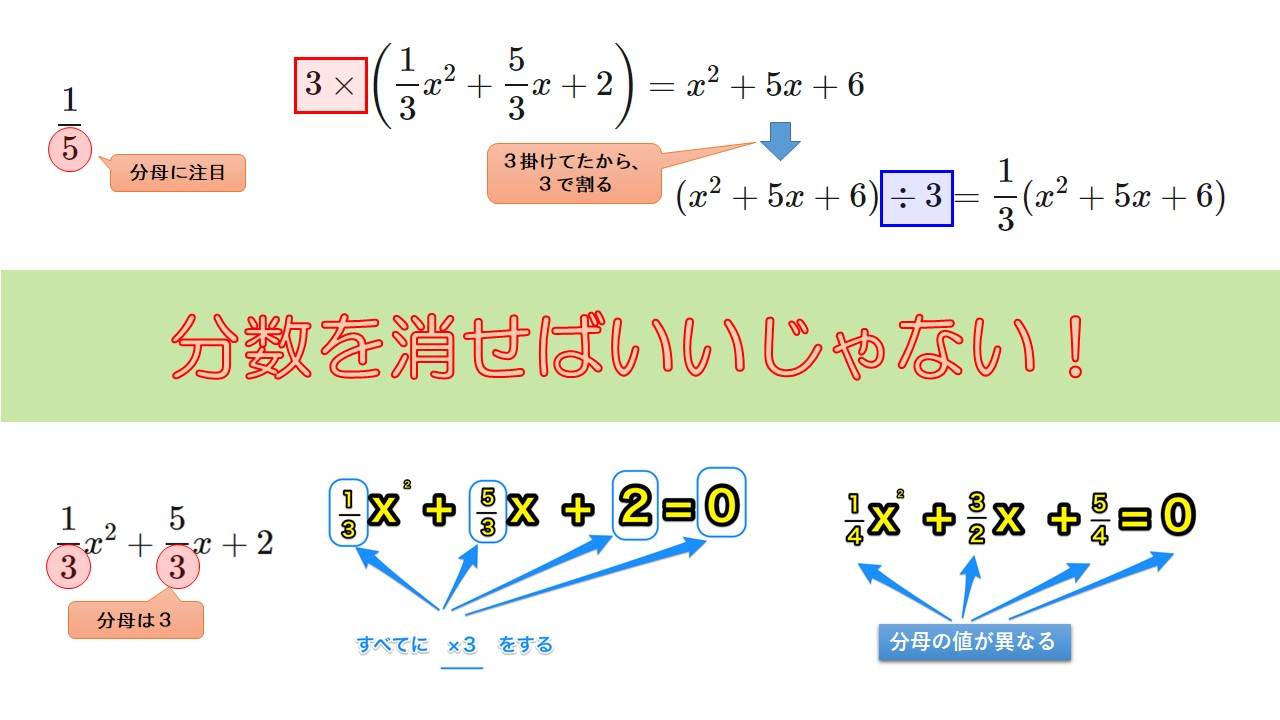



高校数学 因数分解 分数が登場する式を因数分解する方法 わかりやすく解説します 数学の面白いこと 役に立つことをまとめたサイト




今年も因数分解コンクール 最近の出来事 英国 イギリス留学生へのキリスト教に基づく全人教育 立教英国学院 Rikkyo School In England




無料 中3数学 基本問題 問題プリント 305 式の計算5 因数分解1




解けますか ちょっと難しい因数分解 暇つぶしに動画で脳トレ



Studydoctor2乗の因数分解 中3数学 Studydoctor




中3 数学 因数分解 共通因数でくくる 無料学習プリント教材




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ




改訂版 3trial数学 P14 3 因数分解 練習問題




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解




数学 質問解答 4乗 を含んだ因数分解 難問 最終話 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生




モノマナビ研究所




勉強しよう数学解答集 因数分解の応用問題の問2の解答




数学 中3 6 因数分解 Youtube




中学数学 因数分解の解き方と練習問題 Irohabook




因数分解難問と意外な別解 怜悧玲瓏 高校数学を天空から俯瞰する




展開 因数分解を利用する問題 鶴城数人 Note




数学iの因数分解について質問です Clear
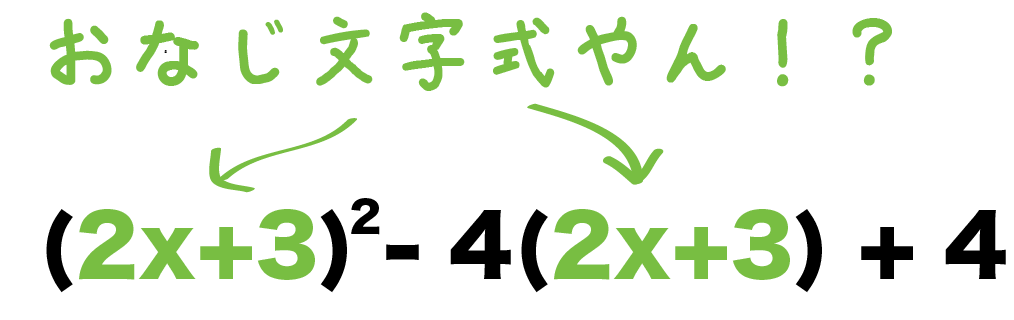



いろいろな因数分解 置き換え問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学の解説5ページ目 三重の個人契約家庭教師




高校数学 複数の文字を含む因数分解は最も次数が低い文字で整理せよ 受験の月




中3 展開と因数分解13 動画 公式を使う因数分解1レベル3の解説 中学数学の勉強に




中3数学の計算問題プリント 式の展開 と因数分解 桜花 現役バイト塾講師 Note




中3 式の計算 因数分解 応用編 基本の理解で組立ok 難問と勉強の取組みについて 教えたい 人のための 数学講座



中3数学 因数分解についてです 下のプリントの問題の解答を作ってくださ Yahoo 知恵袋




因数分解の応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中学3年の数学 動画 因数分解 もっと応用編の問題 19ch




中学数学 因数分解 練習問題集 基礎力養成 数学練習問題集シリーズ 山本権太 数学 Kindleストア Amazon




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解



U9j580gf8iba369ji2w Xyz P 599




中学 数学 因数 分解 シモネタ




因数分解の工夫 2 標 難 組み合わせ 難 二乗 二乗 最低次数整理 数学の解説と練習問題




無料 中3数学 基本問題 解答プリント 305 式の計算5 因数分解1




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学の平方根と因数分解の問題です 説明まで 付けて貰えると助かります Clear




数学 定期テストに出題される因数分解の問題 大学入試数学の考え方と解法



0 件のコメント:
コメントを投稿