三角形の内角の和を求める方法を確認する活動の中で,図をかいたり,作業しながら, 今までの学習内容をおさらいする。 <三角形の内角・外角> <角度の意味> <三角形の3つの角の和の求め方> 360° 180° (小学校の方法) 外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して これは内角を問われる問題なんだけど、外角の性質を利用すると簡単に解くことができます。 まず、1つ分の外角の大きさを求めましょう。 $$360\div 12=30°$$ すると、正十二角形の1つの外角は30°であることが分かりました。 ってことは、内角は

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
内角の求め方
内角の求め方-右の図のように,五角形 abcde があり,頂点 a, c における内角がそれぞれ 114°, 130° であり,頂点 d, e における外角がそれぞれ 78°, 65° であるとき,頂点 b の内角の大きさは何度か。多角形の内角の和の公式は180 (n-2)°です。 nは多角形の辺の数が入ります。 三角形の場合n=3なので180 (3-2)°=180°です。 六角形はn=6ですから内角の和=180 (6-2)°=7°です。 考え方は簡単です。 多角形を三角形に分解して考えます。 四角形は2つの三角形に分解できます。 1つの三角形の内角の和は180°ですから四角形の内角の和=180×2=360°です。 今回は



この方法で星型五角形の五つの内角の和の求め方をおしえてください A Yahoo 知恵袋
多角形の内角の和を求める問題です。 小学生の学習では公式として暗記するのではなく、図形の中に三角形を作って求められるようにしてください。 五角形の内角の和の求め方 考え方1を使うことが多いですが、考え方2の方法も確認しておきましょう。 60×3=180だね。 三角定規はどうだったかな。 角のせいしつ 三角定規 検索 三角定規(直角二等辺三角形):45°・45°・90° 三角定規(直角三角形):30°・60°・90° 三角形の内側の角の大きさの合計の事を「内角の和」といい、全ての三角形は180°です。 三角形の内角の和が180°はわっかったけど、外角の定理って 先生正十二角形の1つ分の内角は\(=150°\) と求めてやることができます。 内角の和を考える方法 次は内角の和から1つ分の大きさを求める方法です。 まず、多角形の内角の和は $$\LARGE{180 \times (n2)}$$ で求めることができましたね。 正三角形の内角の和であれば
内角の和が1440°である多角形は 4 四角形かどうか 5 四角形の中心の求め方 6 なぜ「n」を使うか? 7 4辺の長さが分かっている四角形 8 任意の四角形の4つの角の二等 9 5角形の内角の和は何度ですか? 10 地縄の出し方 11 60°、30°、50°、40°の作図の問題 12 四角形の内角の和が360°であることを理解する。 ※四角形の内角の和の求め方を三角形の内角の和の求め方を根拠にして説明する活動。 習得 12 多角形の用語、意味を理解し、多角形を三角形に分割して内角の和を求める。 球面三角形の内角の求め方 最終更新 21年4月2日 半径 1 1 の球上にある球面三角形の内角 α α は、 によって与えられる。 ここで a,b,c a, b, c がそれぞれ球面三角形を成す弧の角度である (下の図を参考)。
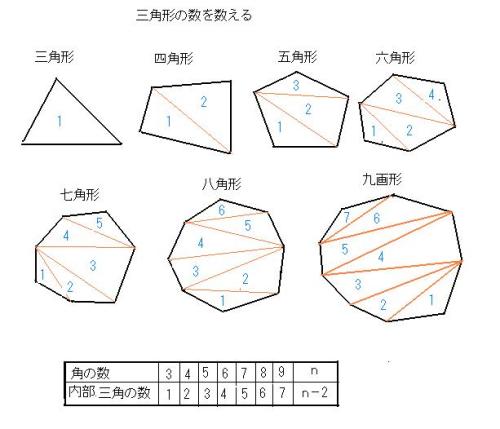
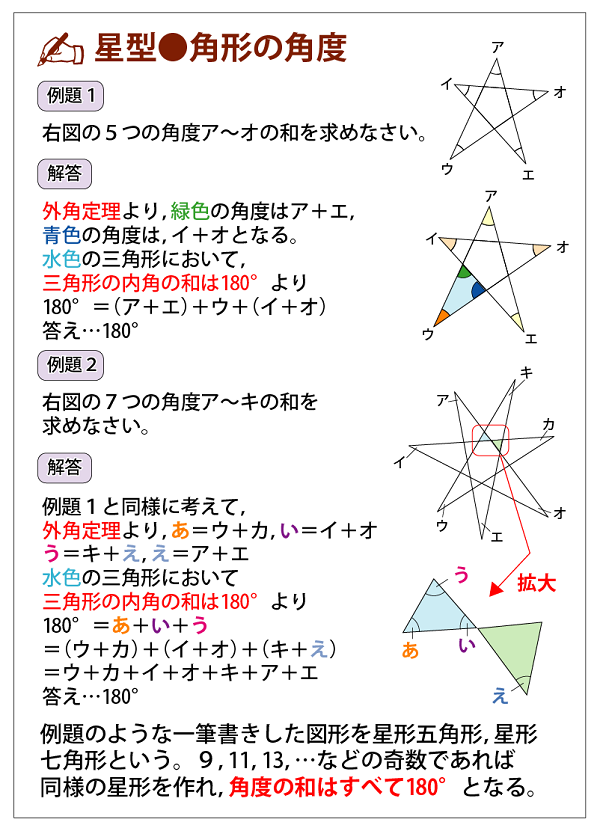
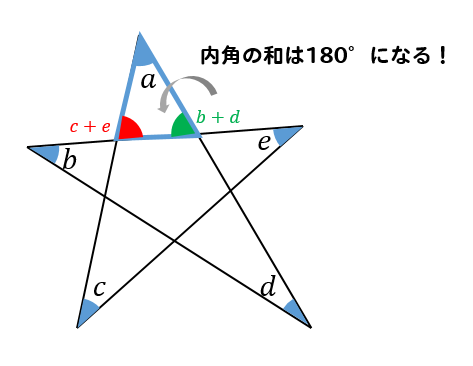
内角の和が180°になることから $$a(bd)(ce)=180°$$ つまり $$\LARGE{abcde=180°}$$ ということになり 内角の和が180°になるということがわかります。 星形の図形では 三角形の外角の性質を利用していくと 全ての角を1つの三角形に集めることができるので 正六角形は対角線で、4つの三角形に分かれるので、内角の和は、 180×(6-2)=7度 正六角形の角は全部で6つあるので、1つの角の大きさは、 7÷6=1度 で求め三角形の数で内角の和が計算できます 五角形と六角形の内部に作成できる「三角形の数」「内角の和」は下の図の通り。 四角形と同じように、三角形の数が分かれば内角の和は求められますよね^^ どうですか? ここまではそれほど難しくないと思います。 多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。 ということで! ここで一気に




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




内角の和から多角形を求めるのってどういうやり方でやるんですか Clear
★無料の中学メルマガ講座★毎週、問題と動画講義をお届け! 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料 多角形の内角の和の求め方 角形の内角の和は次のように求めれます。 例 十角形 ⇒ 十二角形 ⇒ なぜ上のような式で求めることができるのか確認しておきましょう。 三角形の内角の和が180°になるというのは知っての通りだね。 これを利用すると星形多角形の内角とは,多角形 の各辺の延長線でつくられた, 鋭角のみをいいます。 ∠a+∠b+∠c+∠d+∠e を 星形五角形の内角といいます。 星形多角形の内角 星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e)




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




8 2 Descubre Como Resolverlo En Qanda
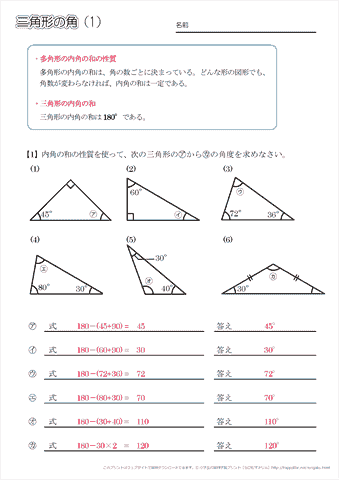
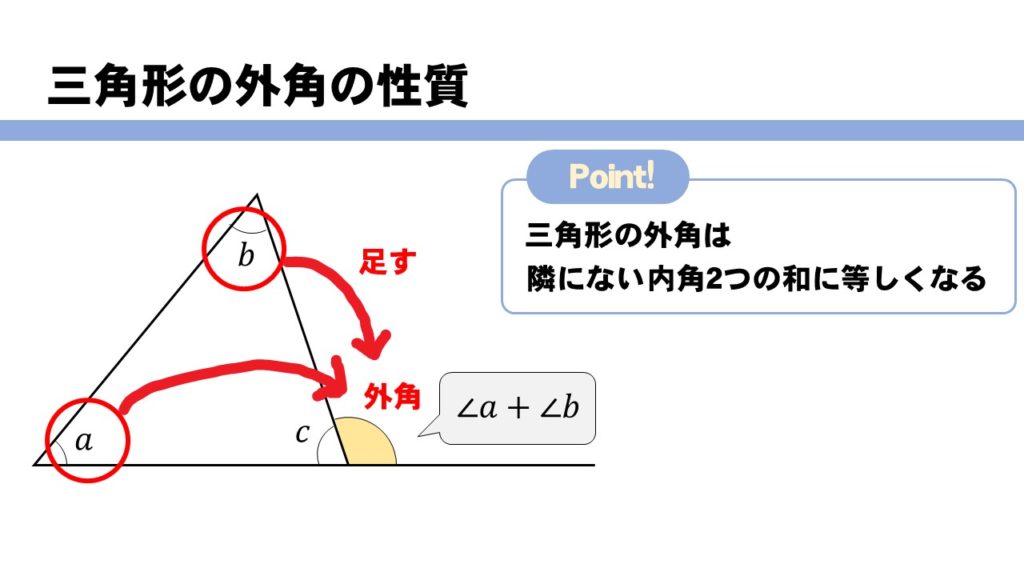
正多角形の内角・外角の求め方を解説! 星形の角度の求め方を解説! ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法!二十角形の内角の和は何度か。 十八角形の内角の和は何度か。 内角の和が 7°になるのは何角形か。 内角の和が 1260°になるのは何角形か。 正十五角形の 1 つの内角は何度か。 正十角形の 1 つの内角は何度か。 多角形の外角の和は何度か。 三角形の内角 三角形の3つの内角の和 → 必ず180°になる 問題 xの角度は??簡単だね?3つの内角を全て足し算すると180°だから、 40°65°∠x=180° ∠x=75° ・・・(答え) 三角形の外角 赤色の角度のことを、ぜんぶ 「外角」 と呼ぶよ!



多角形の内角の和を簡単に求める方法 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



Math 多角形の内角の和 働きアリ The 2nd
三角形の内角の和は180°であることから ABCの内角の和=x+45°+60°=180° x=180°-60°-45°=75° 答え ∠x=75° 問題② 下の図における ∠x の大きさを求めなさい。 この問題は補助線(ここでは∠Cから辺ABに向かい元々あった辺を延長させた線。内角の和・外角の和の証明 なぜn角形の内角の和が180°×(n2)となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習にな こんにちは、ウチダショウマです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こ




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




角度の求め方 算数の教え上手 学びの場 Com
三角形内角求め方, 球面三角形の内角の求め方 この関係式を用いると、 球面三角形の内角を中心角(または弧の長さ)から求めることができる。 関連リンク 球面三角形の面積 4点を通る球を求める例題 正n角形の内角の大きさの求め方画像の説明がまったく理解できないのですが、式の意味を教えて下さい。多分 133ページには、こんなようなことが書かれていた筈です。四角形の 一つの頂点から 他の頂点の線を引くと、2つの三角形が出来ます第5学年算数 三角形の内角の和を基に四角形の内角の和の求め方を考え,筋道立てて説明す る。 1 単元名 図形の角 2 単元のねらい (1)三角形の内角の和を調べ,どんな三角形でも180°になることを説明することができる。




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



5年 三角形のふしぎ 算数イメージ動画集 大日本図書
一方、多角形の内部にできる角を「内角(ないかく)」といいます。 三角形の場合、内角の和は180度になります。 今回は外角の意味、求め方、内角との違い、外角と内角の和について説明します。 内角の和、内角の意味は下記が参考になります。 内角の和と三角形の関係は? 1分でわかる和の値、証明、外角との関係 100円から読める! ネット不要!でも、内角の和は求められます。 しかしその公式の意味を知っている方は多くないと思います。本ホームページでは公式の意味や公式の導き方を図を使用して分かりやすく説明しています。 これで計算するのが楽しくなるかもしれませんよ。 さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。 中心角はつぎの3ステップで計算できるんだ。 Step1 扇形の中心角をx°とおく まずは「扇形の中心角」を「x°」とおいてみよう。 これは 方程式の文章題 と同じ。 Qikeru:学びを楽しくわかりやすく 5 Pockets 方程式の利用一次方程式の文章題の4つの解き方



Nitter




多角形の内角の和の求め方 中学数学 By じょばんに マナペディア
多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されます。え方を a3 用紙にまとめさせ る。その際、何を根拠にして 求めたのか書かせる。 ・班で1枚にまとめる。 ・どの班も同じ方法でまとめて いる場合は、別の方法を書か せて、全体に示す際になるべ く多様な考え方が出されるよ うにしたい。多角形の内角の和・外角の和は?正多角形の内角の求め方は ポイントは、内角と外角の和は簡単に 180°×n 180 ° × n と求めることができるところですね。 なぜなら、 n n 角形の頂点の個数は n n 個だからです。 これは多角形の外角の和の研究です。



この方法で星型五角形の五つの内角の和の求め方をおしえてください A Yahoo 知恵袋



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
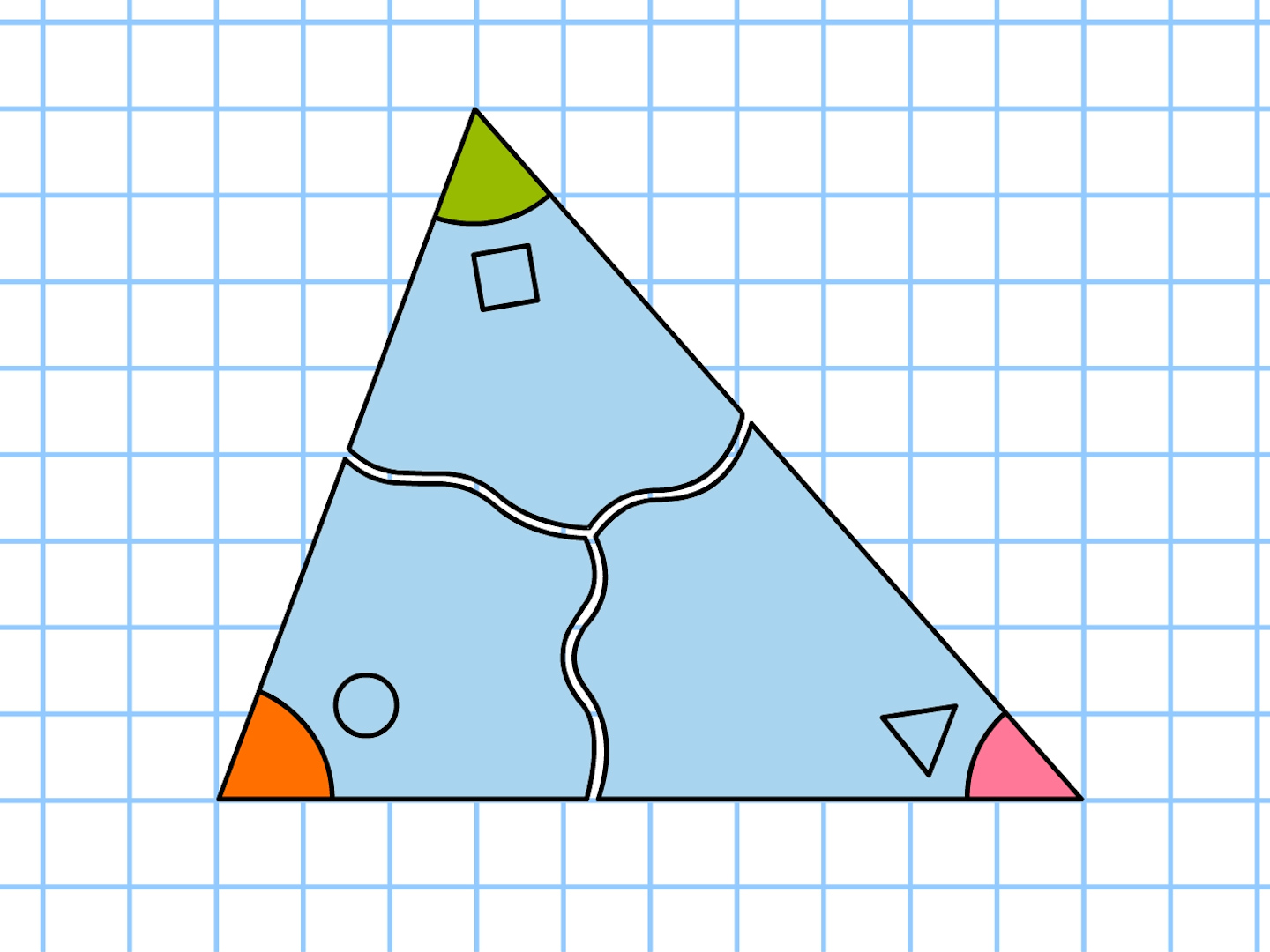
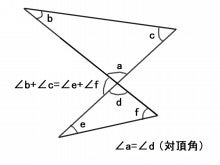
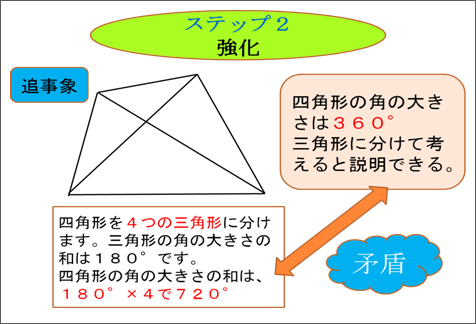
②三角形の内角の和が 180°であることと対 頂角は等しいという性 質を利用することで, 三角形の内角の和と等 しくなり180°である ことがわかる。 ③三角形の外角の性質と 平角が180°であるこ とを利用して,180°で あることがわかる。




課題学習の指導 数学



図形の扉 三角形の外角の定理




小学校5年 算数 正多角形の角の大きさ Youtube




内角の和 と 外角の和 名寄 算数数学教室より



3分なるほど 三角形の内角 外角の性質について解説 数スタ




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




内角の和が2340度である正多角形の一つの外角の大きさを求める問題の答えが24度なん Clear




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




動画で学習 2 多角形の角 数学
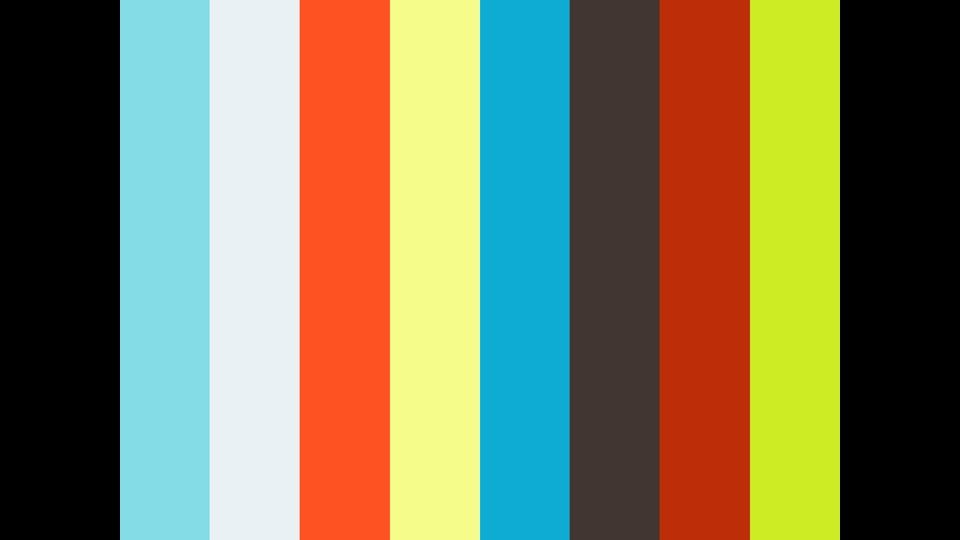



4章1節04 三角形の内角の求め方 中村 翔
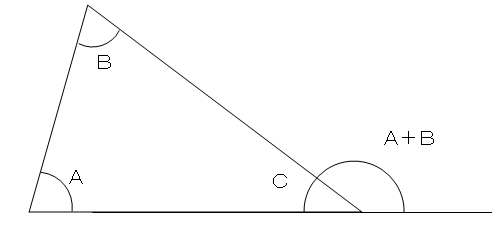



三角形の内角と外角の関係




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



五角形の内角の和の求め方 久保塾 今治市の学習塾



内角の和が540 7 900 1080 1260 の多角形は何角形か




三角形の角度を求める問題 小学生 中学生の勉強
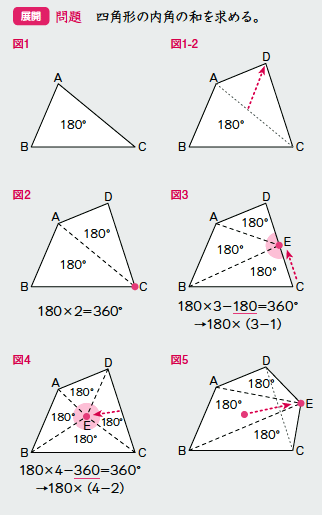



活用 の視点を取り入れた授業例 2 図形の性質 四角形の内角の和 5年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所




内角の和




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題



多角形の内角の和は 1分でわかる公式 問題の求め方 簡単な証明




図形の調べ方 N角形について 内角の和を求める 苦手な数学を簡単に




中2数学 三角形の内角と外角 例題編 映像授業のtry It トライイット




3 Descubre Como Resolverlo En Qanda



3
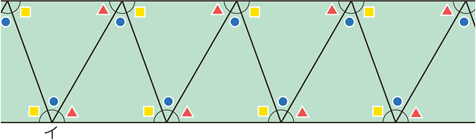



内角の和 算数用語集




三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
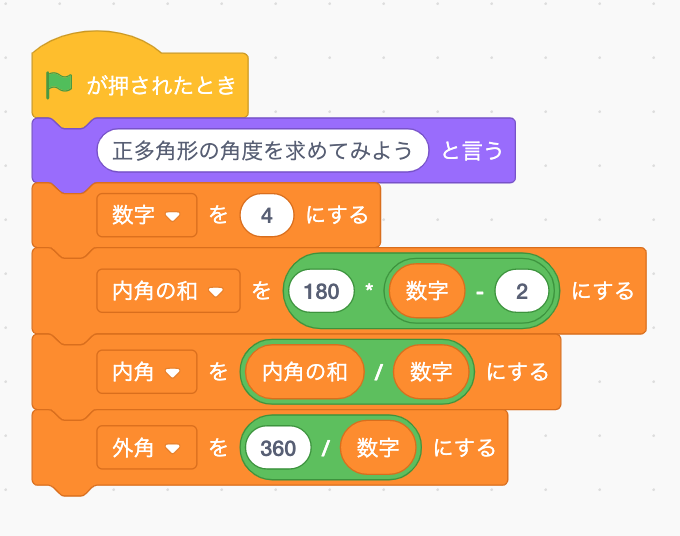



Scratch プログラミングで正多角形の内角 外角を求めてみよう いなきたものづくりラボ




三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
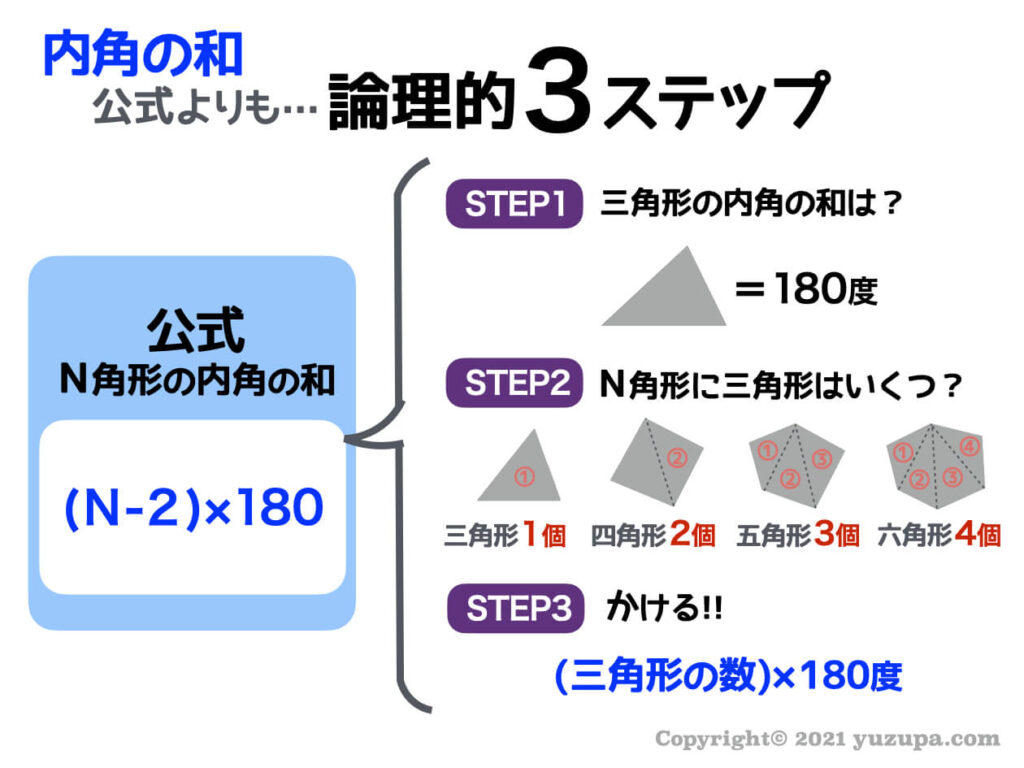



中学受験 多角形の内角の和 公式を忘れなくする論理的3ステップ かるび勉強部屋




多角形の内角の和 外角の和の公式 数学fun




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear
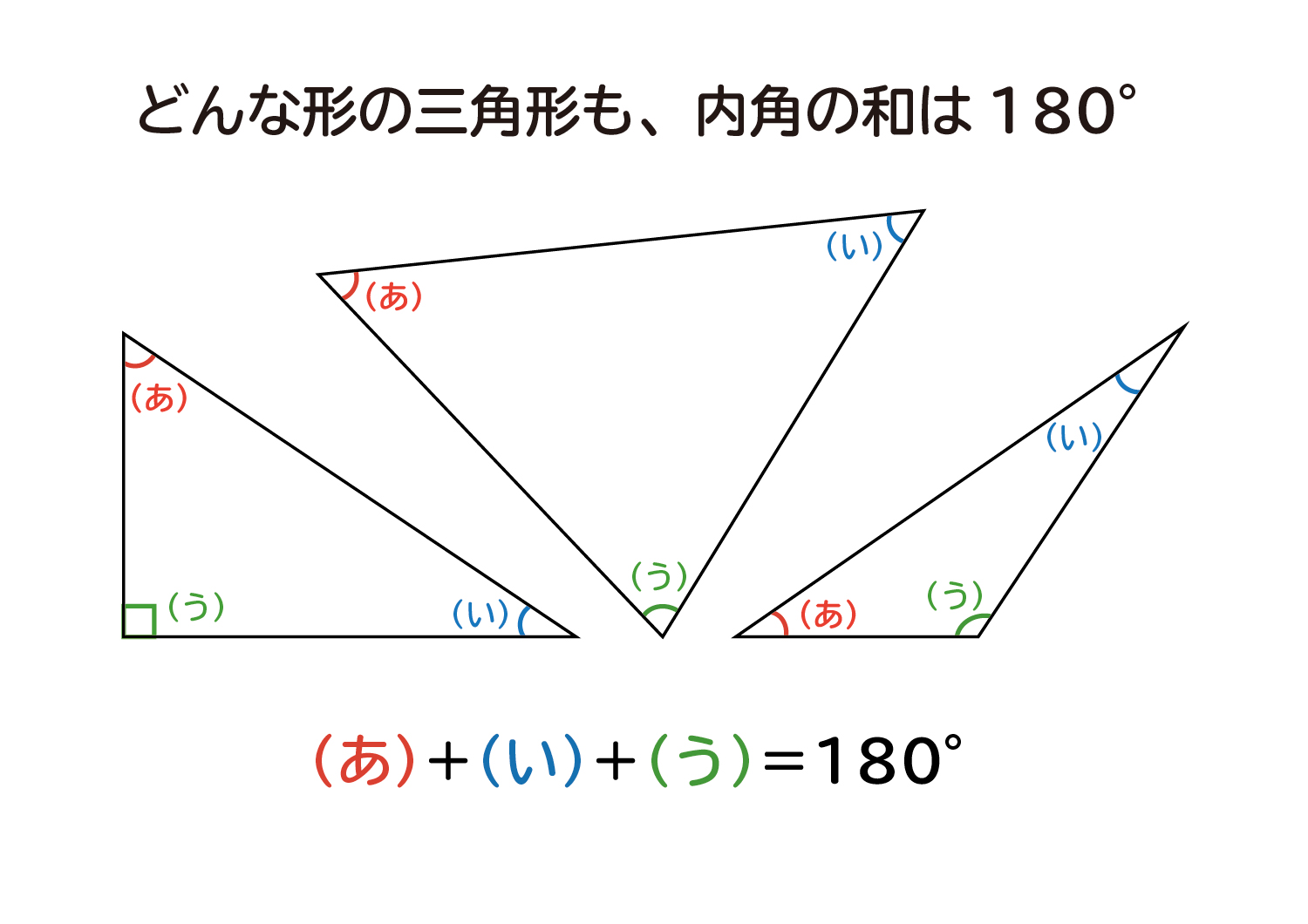



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル



外角とは 1分でわかる意味 求め方 内角との違い 外角と内角の和




多角形の内角の和 は何度なのか を説明します おかわりドリル
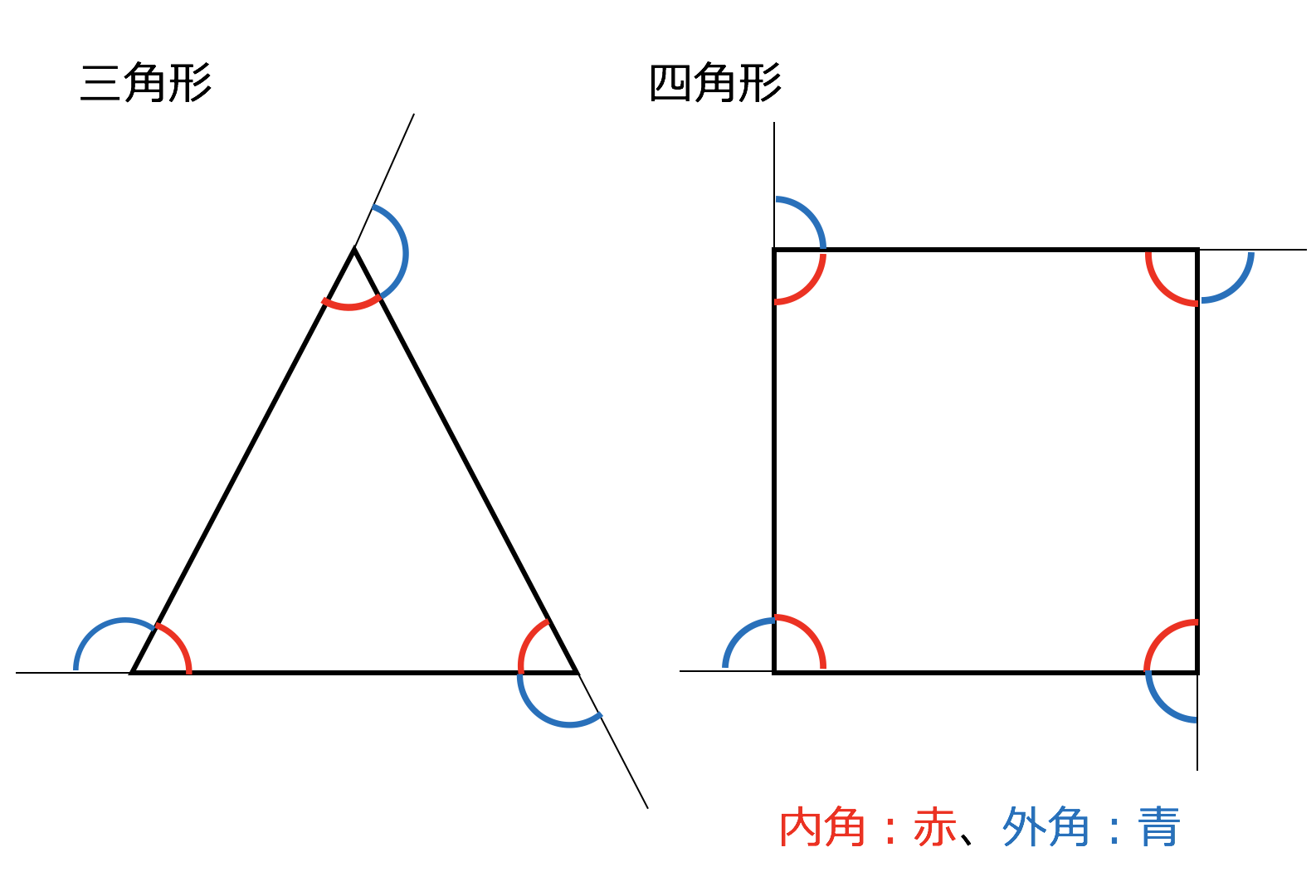



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




小学校5年 算数 四角形の内角の和 Youtube



1



星型 角形の角度の問題 恋する中学受験 大学受験を見据えた中学受験



多角形の内角と外角 思考力を鍛える数学



角度の求め方 数学が嫌いなんです




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



Studydoctor多角形の内角の和 中2数学 Studydoctor



2



数学教育 幾何 図形 的見方 多角形



星形の角度 内角の和の求め方を問題解説 数スタ
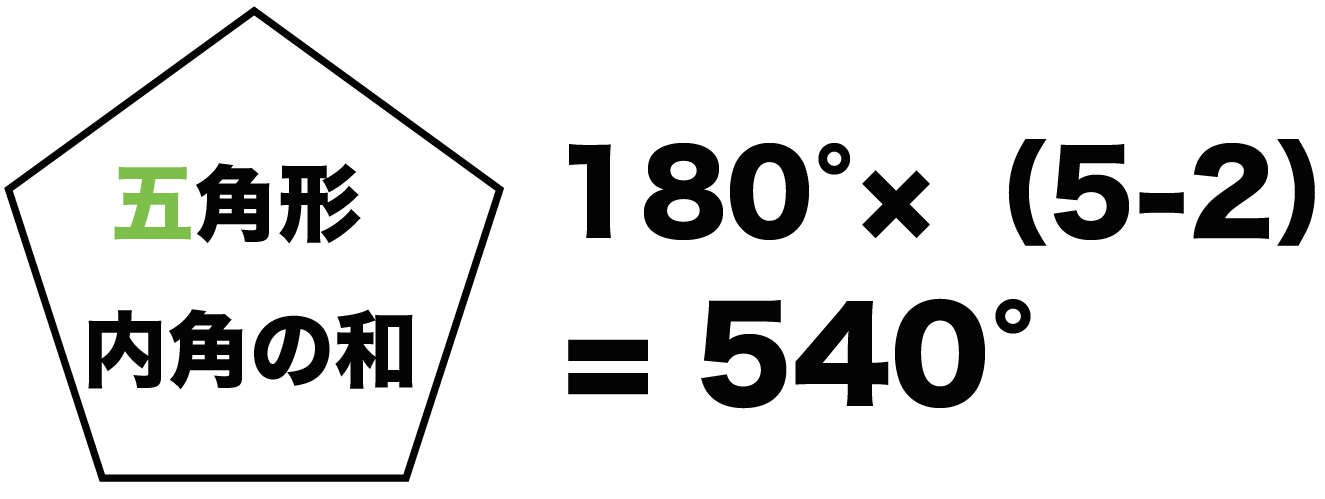



中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
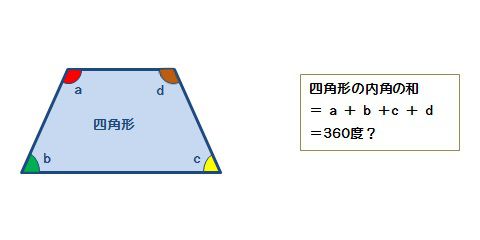



四角形の内角の和 算数の公式覚えてますか
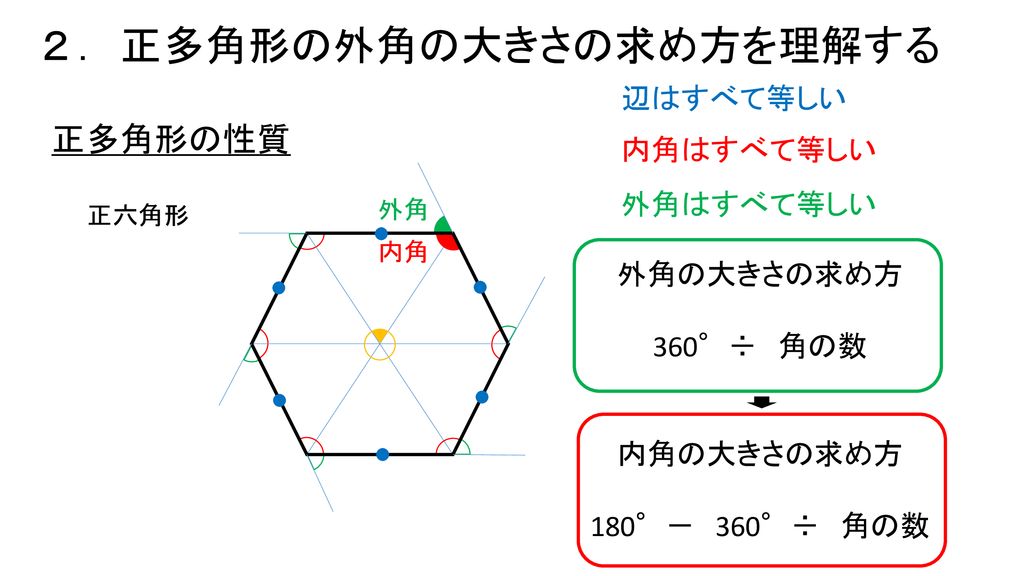



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




球面三角形の内角の求め方 理数アラカルト




内角の和 180 N 2 外角の和 360 教遊者




多角形の内角の和 は何度なのか を説明します おかわりドリル




多角形の性質 中学受験準備のための学習ドリル




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ




数学 中2 48 三角形の内角と外角 基本編 Youtube




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
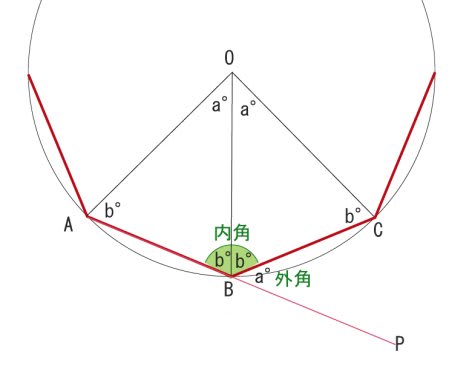



内角 と 外角 って 何だっけ 名寄 算数数学教室より
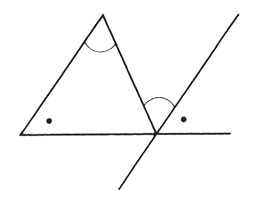



内角の和 算数用語集




中学校数学自宅学習2年 多角形の外角 星形五角形の内角
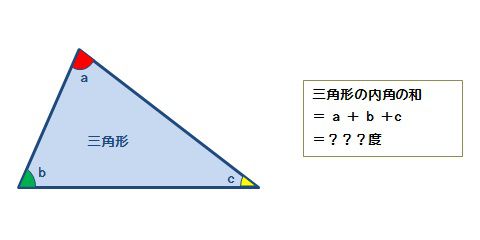



三角形の内角の和 算数の公式覚えてますか
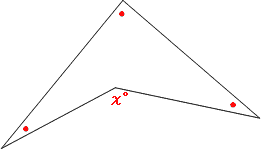



角度の求め方 算数の教え上手 学びの場 Com



中二 五角形の内角の和の求め方 をアップ 久保塾 今治市の学習塾
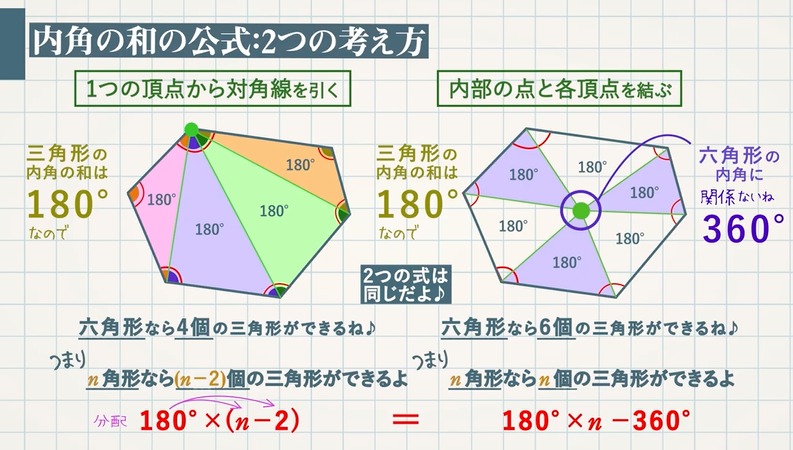



内角の和 180 N 2 外角の和 360 教遊者
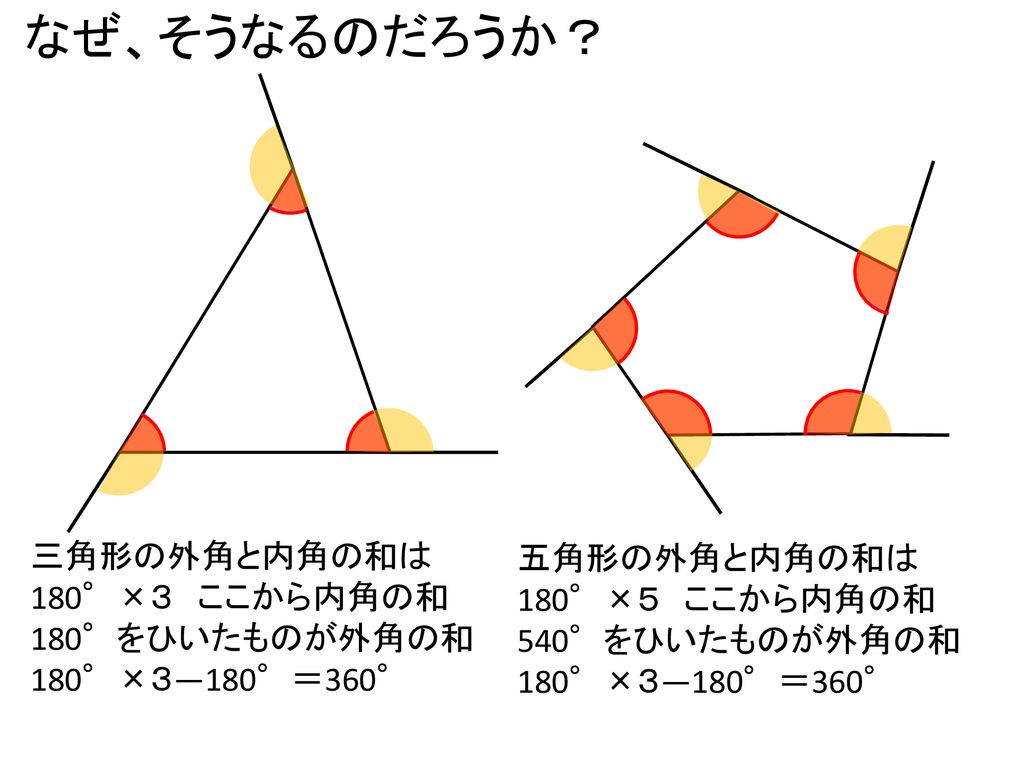



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
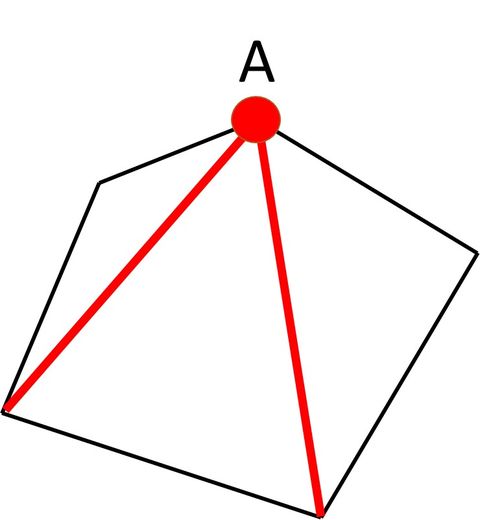



多角形の内角の和はなぜ n 2 のぶちゃん先生の花まる教室



中学二年生の星形五角形の内角の和の求め方を教えてください 星 Yahoo 知恵袋



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス
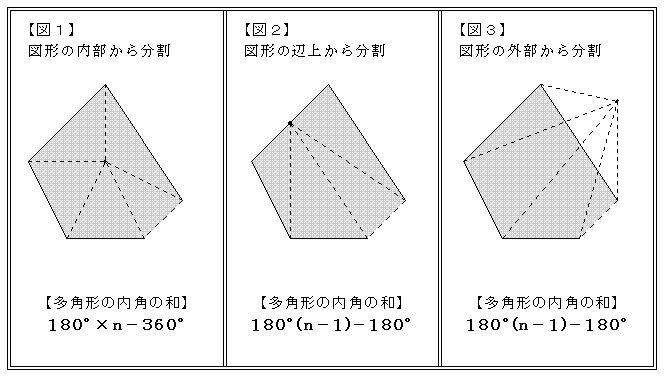



多角形の角
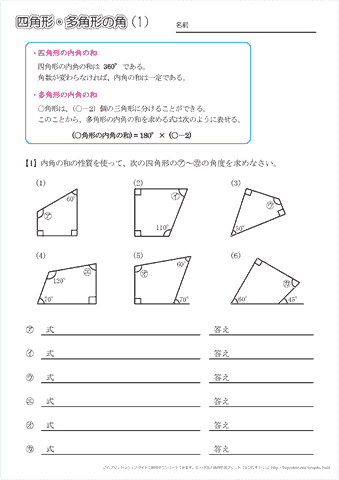



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋
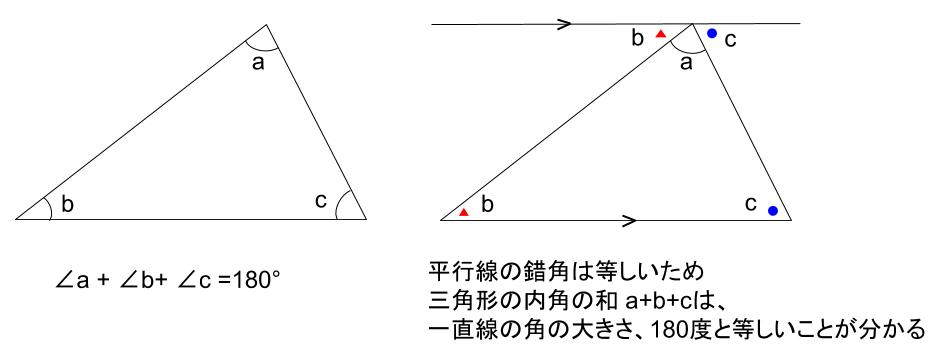



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




多角形の内角の和 算数の公式覚えてますか



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




中2数学 多角形の内角 外角 図形の合同 ひっそりと物理や数学を解説する




三角形の内角の和を帰納的 演繹的に求める方法 算数を究める



1




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題
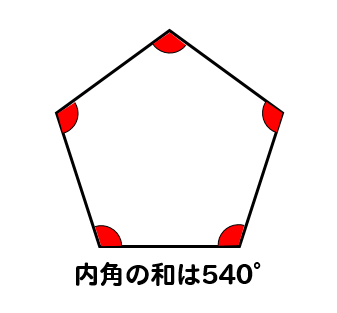



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



1



中2数学 多角形の内角の和 外角の和まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




多角形の内角の和の公式と外角の和を利用した角度の求め方




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく



Http Www Asahikawa Hkd Ed Jp Asahi Els 08 a5m as Pdf



0 件のコメント:
コメントを投稿