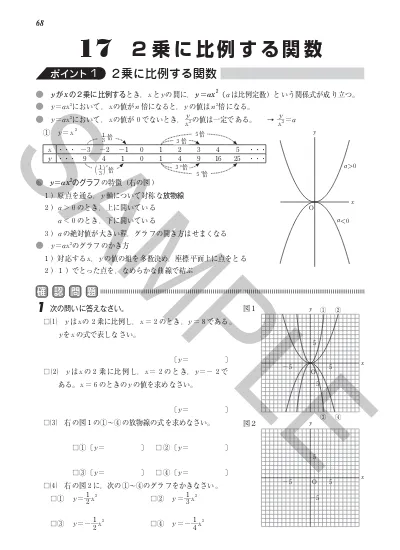
OMu 0 (MI必ジ フがヶy軸の上側には出ない もの 拓。 (3 グフクンがの 軸について対称である関数の組 04Z* WW ルッデー02ア (》) グラフがヶ軸の下側には出ないもの (9 '間 (4) グラフの開き方が最も大きいもの イ2乗に比例する関数のグラフは直線ではないため、 できるだけたくさんの点をとりフリーハンドでなめらかな曲線のグラフをかく。 y= 1 4 x 2 のグラフの書き方 xの値を式に代入して下の表を埋める。 → x 8 6 4 2 0Y 軸に日付をもつ横棒グラフを作成します。y 軸の範囲を 14 年 6 月 1 日から 14 年 6 月 10 日までに設定します。 次に、ylim の最初の入力引数として ax2 を指定することで、下のプロットの y 編集された方の例を開きますか?
Y Ax 2
Y=ax2 グラフの開き方
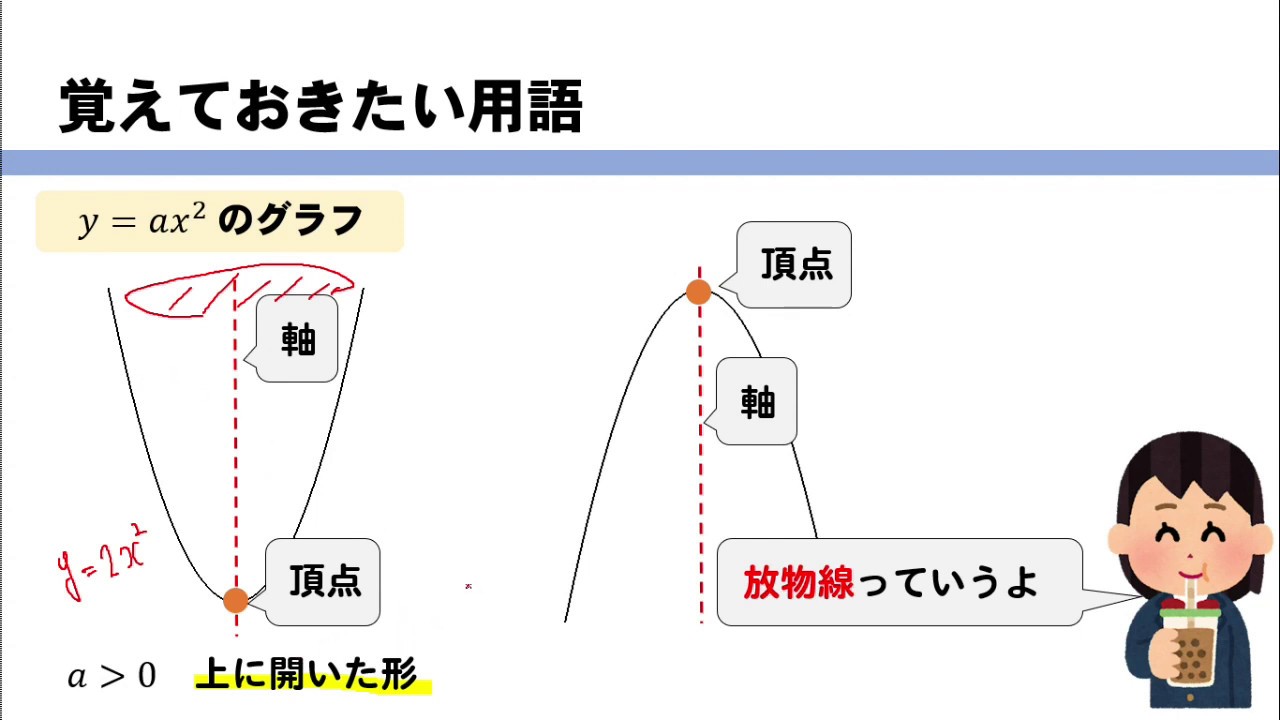
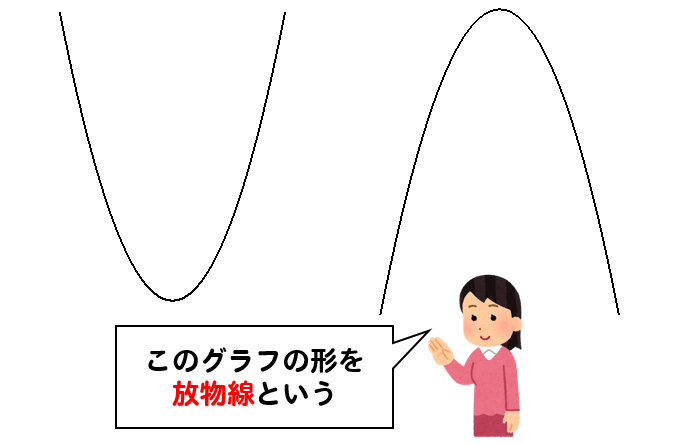
Y=ax2 グラフの開き方-「比例定数の求め方」 正比例と同じだが、y=ax2 の式にxとyの値を代入して求める。 「y=ax2 のグラフ」 放物線と呼ばれる曲線となる。 原点を通り、y軸について対称となる。 a>0のときは、上に開き、a<0のときは、下に開く。・関数y=ax2の意味を理 解している。 ・関数y=ax2のグラフや 変化の割合などの特徴を 理解している。 ・具体的な事象の中で,関数 y=ax2の用い方を理解グラフの頂点は、"y=ax²bxc"を平方完成して"y=a(x−p)²+q"の形にすることで求めることができましたね。




基礎数学のこの問題を教えてください Clearnote
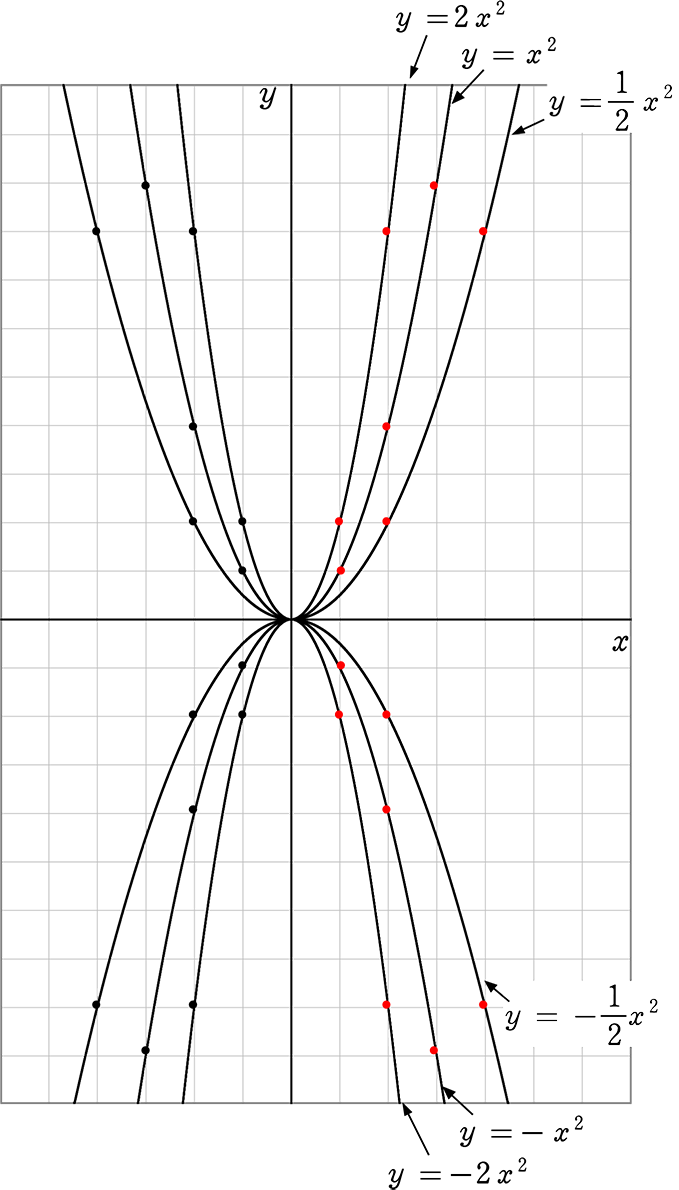
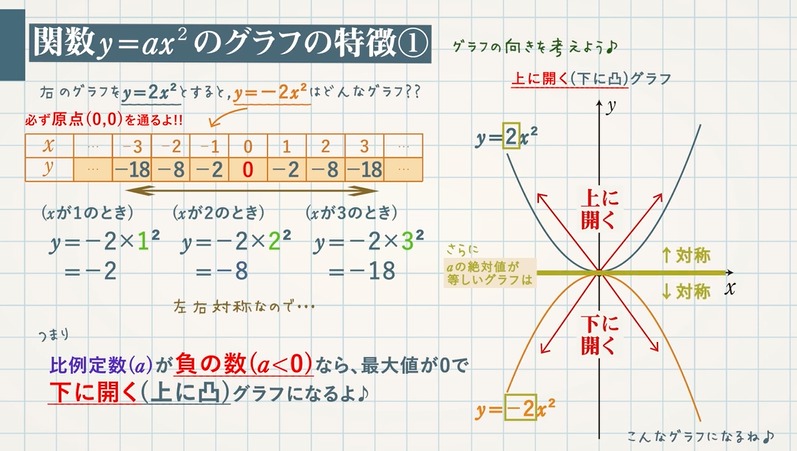
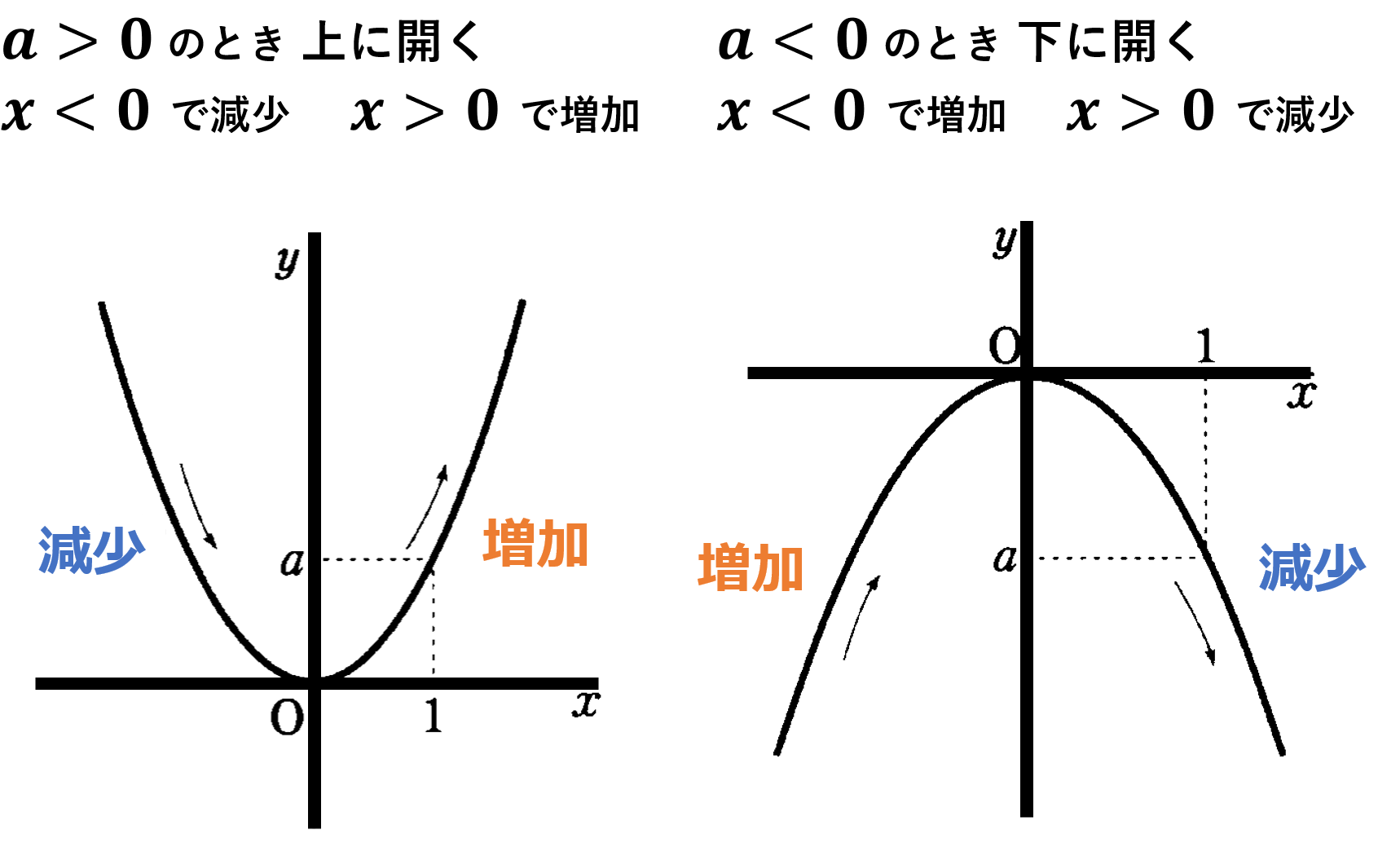
数量についての知識・ 関数y=ax2の表,式,グラフの特徴やその関連について理解し,知識を 理解 身につけている。 5 指導方針 ・速さが一定でないことが理解できるように,球の転がり方を表にまとめるようにする。Y=ax二乗のグラフの書き方Y=ax 2 のグラフの特徴 必ず原点を通り、その原点が頂点である。 y軸について対称である。 a > 0のときは上に開き、a 0のときは下に開く。 aの絶対値が小さいほどグラフの開きが大きい。Y=ax2 のグラフ ① 原点を頂点とし,y軸に関して対称な放物線となる。 ② a>0のとき,上に開いている。(下に凸ともいう) a<0のとき,下に開いている。(上に凸ともいう) ③ aの絶対値が大きくなるに従って,そのグラフの開き方は 狭くなる。
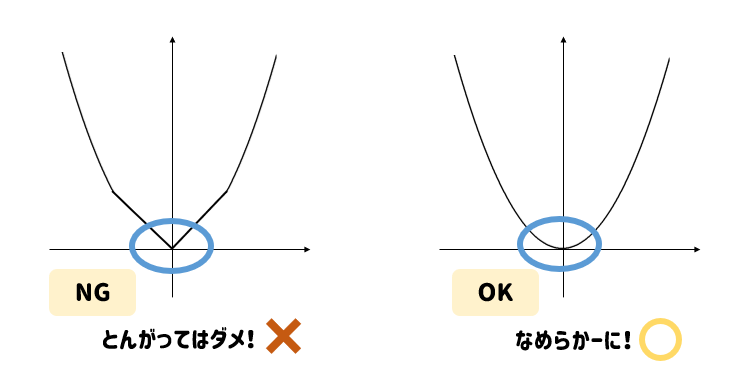
記録テープの実物には、適切な打点(0,1,2,3,4,5,6,7,8,9,10,11,12)を赤チョークで先生が書くこと 次に、定規で記録テープ各打点から真横に補助線をひきます。 そして、グラフ横軸の各目盛り(1~12)から真上にひいた補助線との交点を求めます(上図)。 理想的な実験(摩擦0)の場合、6打点目(01秒後)は49cm、12打点目(02秒後)は196cmになることを知らせます。 y'=2ax,y''=2a y''の符号はグラフの凹凸を決めるので,aは曲率に関係する量と言えます.一般に曲線y=f(x)の曲率とは, y''/{1y'^2}^{3/2} をいいます.放物線のグラフの特徴 放物線グラフの書き方 分数の場合の書き方 y=ax2乗のグラフ書き方 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがで
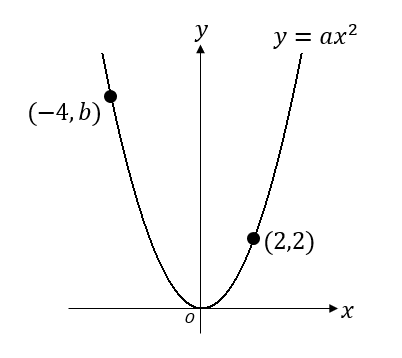
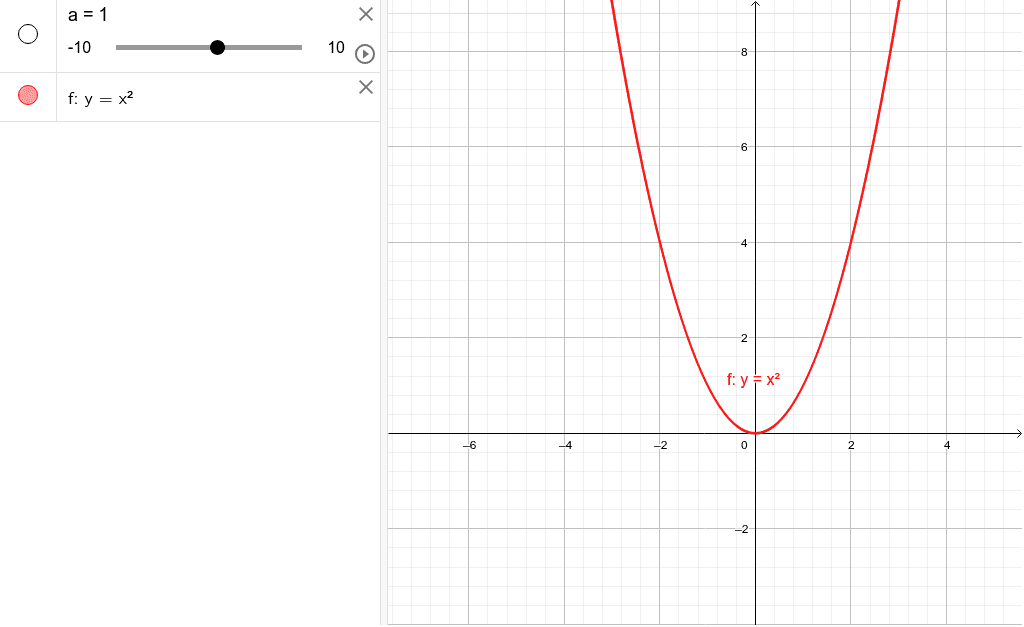
2乗に比例する関数のグラフ(放物線)の書き方 y=ax2 のグラフの書き方の問題です。 2次関数のグラフがスムーズに書けるようになることは、高校生になっても必要になります。しっかり練習するようにしてください。 関数y=ax2 グラフの交点 関数と方程式のネットワークをつくろう! 図形の相似 相似顕微鏡 相似のイメージを豊かにしよう! 円周角と中心角 くるくる四角形 円に内接する四角形の性質を見つけよう! 三平方の定理 どのくらいまで見えるかなA(6, 9) B(1,3) ←点Aを通るとき ↓aの絶対値が大きいほど 開き方が小さい x y O aの絶対値が小さいほど ↓開き方が大きい y=ax 2 のグラフは, aの絶対値が小さいほどグラフの開き方が大きくなる。 そのため, 図のようにグラフが点Aを通るときにaの値が最小となる。 y=ax 2 にA(6, 9)を代入すると 9=a×(6) 2 36a=9 a= 1 4



数学の入試の過去問です 関数y Ax2乗で Xの変域が 4 X 2のとき Yahoo 知恵袋



Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト
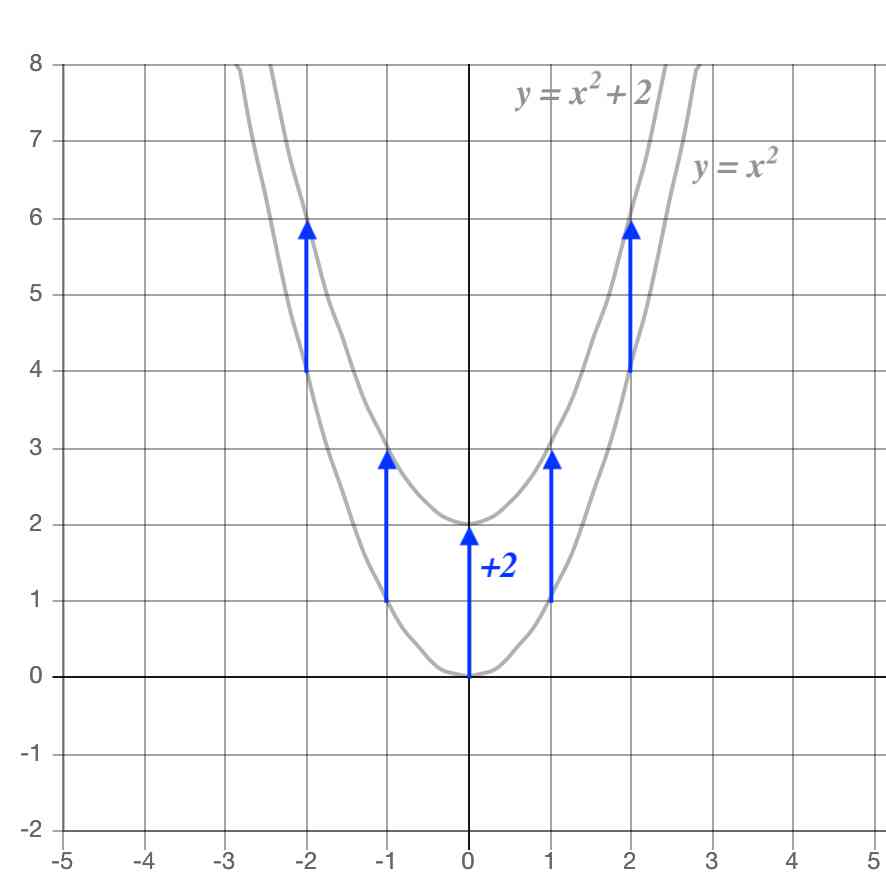
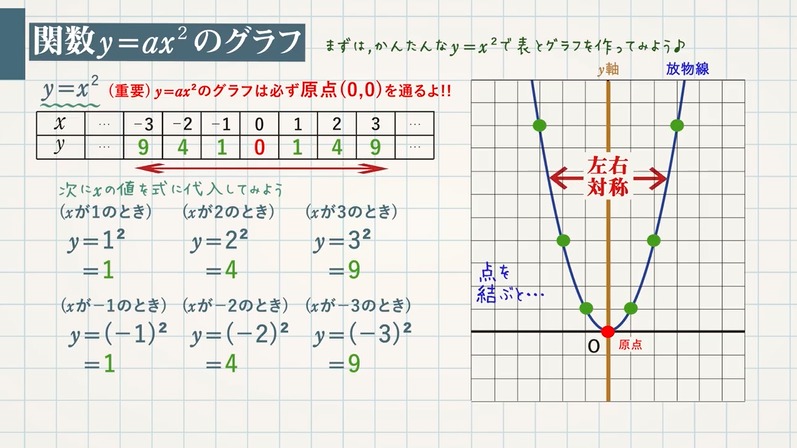
a に「 2 」を入れれば「 y=2x2 」になります。 これは、「 y は x の二乗の 2 倍」にすぎません。 先ほどの「 y=2x 」の「 x 」が「 x の二乗」に変わっただけです。 二乗は「同じ数を掛ける」だけなので、難しくありません。 「 y は x の二乗の 2 倍」ならこうすればよいわけです。 ・ x が 1 なら y は 1 に 1 を掛けて 2 倍にするだけだから 2 ・ x が 2 なら y は 2 に 2 を関数 y=ax2 のグラフの特徴 ・原点を頂点とする放物線で,y軸について対称になっている。 ・a>0 のときは上に開いた形,a 使用する グラフの データのインポート で インポートツール が開きます。データの確認と、欲しいデータの選択をしましょう。 % 円グラフの描画 p = pie(ax2,sum(pop10{,35}));



中学数学 関数




2次関数のグラフ
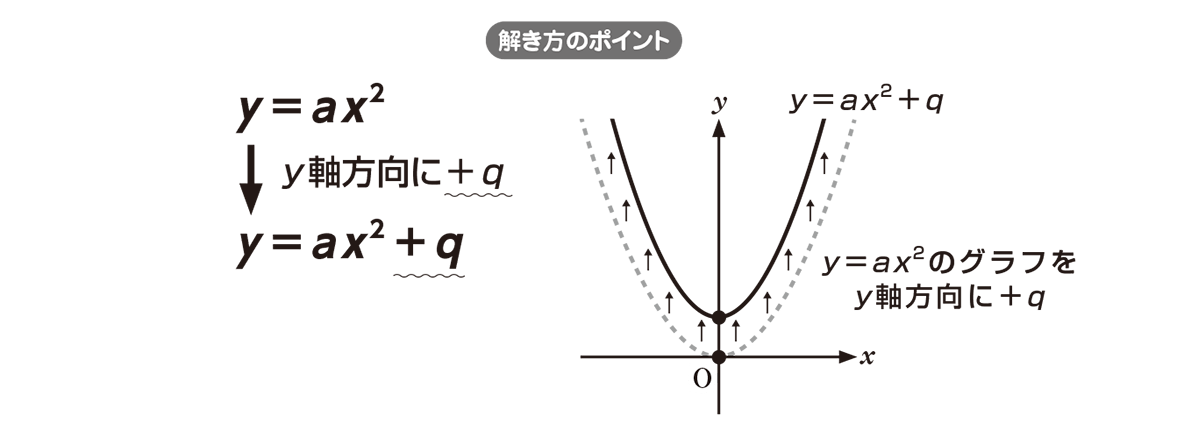
形態:教師提示 〔目標〕 (1) 中学校で学習したy=ax2のグラフの形を復習し,軸,頂点,aの正負による上下に凸という用語を理解する。 (2) y=ax2のグラフとy=ax2qのグラフとの関係を,グラフの平行移動という見方から理解する。 基本のポイント 必ず原点を通り、その原点が頂点である y軸について対称である a > 0のときは上に開き、a < 0のときは下に開く aの絶対値が小さいほどグラフの開きが大きい y=ax2のグラフとy=ax2のグラフはx軸について対象である。 2次関数 y=ax²bxc の係数はそれぞれグラフの様々な要素に関係します。 a グラフの開き具合 , 上 or 下に凸 b グラフの位置(x軸方向/y軸方向) c y切片 , グラフの位置(y軸方向) 詳しいことは「2次関数 係数 意味」で検索してみるといいかもしれません。




中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット




y が x の2乗に比例する関数のグラフ 算数 数学が好きになりmath
三平方の定理より ∠OAB=∠OBA=x 二等辺三角形の底角は等しいので 出発してからの時間をx秒とすると y=ax2のグラフで、yの変域が正なのでa>0である。 図より,放物線の最小値はy=0, 2p2 = 2×52 = 12<関数y=ax2 のグラフの特徴> <グラフの開き> ・線対称、線対称、x軸の上側にあるということ を記載 y=2x2 のグラフとy=x2 のグラフを比べる →y=1 2 x2 のグラフ →y=ax2 で、aある二次関数のグラフを言葉だけで説明するとき、最もわかりやすいのは、 グラフの形と位置 について説明することだと思います。 では、グラフの形や位置と、 `y = ax^2 bx c` という式はどんな関係になっているのでしょうか。




年度用 中学校数学教科書内容解説資料 未来へひろがる数学



Y Ax 2
② グラフの開き方が最も小さいもの ③ グラフの開き方が最も大きいもの 問1. (2) の解答欄 問2. 右上の図に示されるア~ウのグラフの式をそれぞれ求めなさい。形態:教師提示 〔目標〕 y=ax2のグラフとy=a(xp)2のグラフとの関係を,x軸方向へのp平行移動という見方から理解する。 〔指導時間〕 1時間 y=ax2のグラフとy=ax2qのグラフ 1時間(本時) y=a(xp)2のグラフ 1時間 y=a(xp)2qのグラフと平行移動(記号の中の式)=0となるxの値が場合分けのポイント 9、2次関数のグラフ ・CHART&GUIDE、2次関数のグラフの位置関係 y=ax2→平行移動→y=a(xp)q x軸方向にp y軸方向にq ・CHART&GUIDE、y=a(xp)2qのグラフ 頂点(p,q) 頂点の原点とみて、y=ax2のグラフを書く。 ・CHART&GUIDE、y



1



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット
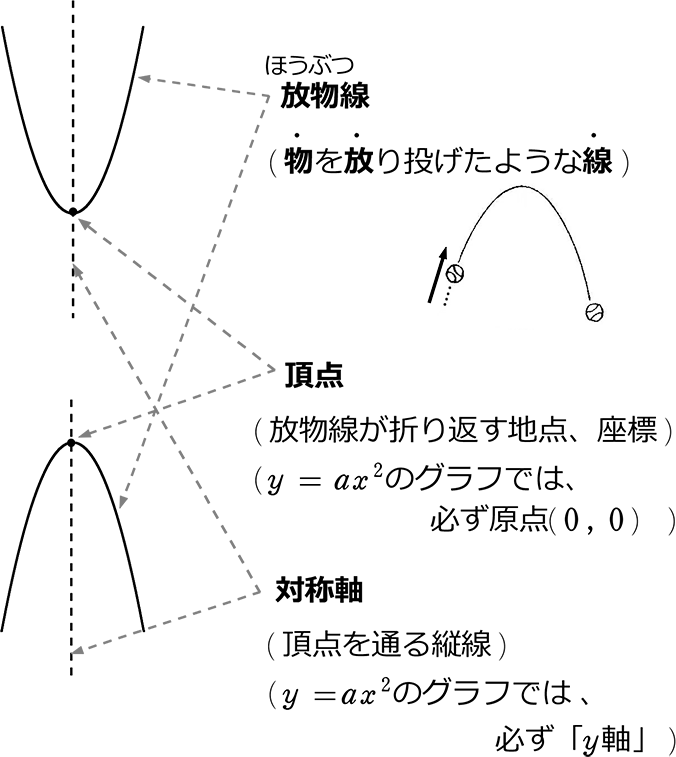
Yはxの2乗に比例する関数 変化の割合二次関数y=ax2の裏ワザ公式 接線 放物線と 例えば, ・・・(A)のグラフ上の点を(X, Y)とし,(A)のグラフをx方向に3,y方向に4だけ平行移動してできるグラフを(B)とすると ・・・(B) これらの図を書いて対応関係を考えると分かるでしょう. この説明に対して「fはどこに行った?この他,放物線y=ax2 のグラフの特徴として,次のことも覚えておきましょう。 ・y軸について対称である。 ・aの値の絶対値が大きいほどグラフの開き方は狭くなる。 aまず,比例定数 の値を求め, yをxの式で表す。



Edu City Fukuyama Hiroshima Jp



関数 中3
・aの値によってグラフの開き具合が決まる ・y=aχ2とy=一aχ2のグラフはχ軸対称 O y = x 2のグラフのかき方を復習 し、比例定数の違う関数のグラフを かく。 ☆y =χ2のグラフをもとに、共通点 とa>O、a<Oの場合に分けられ ることを確認する。 比例定数を4章1節関数y=ax2 関数とグラフこれまでに学んだ比例や反比例,一次関数とは違う新しい関数について学びましょう。 下の写真は,ボールが斜しゃ面めんをころがるようすを,01秒ごとに写したものです。 どんな関係になっているかな? みんなで話しあっ 2次関数式の y=ax2bxcの式から、 xを求める式を教えていただけないでしょうか? y,a,b,cは、判っているのですが、xを求めるのは、どういう式に変換すれば、いいのでしょうか? ど




中3 中3数学 2次関数 1 中学生 数学のノート Clearnote



Y Ax 2
Y=ax 2 のグラフを,x 軸方向へ p,y 軸方向へ q だけ平行移動する。 そこで,X=xp,Y=yq とおくと,x=Xp,y=Yq となるので,与式へ代入すると,Yq=a(Xp) 2A quadratic equation can be solved by using the quadratic formula You can also use Excel's Goal Seek feature to solve a quadratic equation 2 For x = 2, y = 25 3 二次関数の一般式は y=ax^2bxc です 例 2次式 y=ax2bxcのグラフ スピンボタンを利用して係数 a, b, c の値を変化させ、2次式 y=ax2bxcの文章読解問題があるので分量はやや多い感じがしますが、出題の難易度はこちらも易しめでした。普段から英文を読み解く訓練が必要です。 数学 知識問題 y=ax2(aの絶対値とグラフの開き方・放物線・最大値・最小値・変化の割合) 相似(対応する辺・角)



二次関数のグラフの書き方



2乗に比例するグラフ 中学から数学だいすき
まとめ:二次関数y=ax2のグラフの書き方は3ステップでイケル! 二次関数y=ax2の書き方はどうだったかな?? きれいな二次関数の放物線のグラフをかくコツは、 たくさん点データを求めること。 これにつきるかな。 雰囲気の部分がすくなくなるからね。 関数y=ax2のグラフをかこう 関数y=ax2のグラフのまとめ 関数y=ax2のグラフの利用 2関数y=ax2の値の変化 変域(グラフを作成して求めるやり方) 変域(グラフを作成しないで求めるやり方) 変化の割合 変化の割合の利用1 変化の割合の利用22次関数の各係数の意味 1次関数 y=axb の a は傾きを b はy切片を表していたが、 2次関数の各係数は、グラフのどのような特徴を表しているのだろうか? 係数 a の意味 係数 b の意味 係数 c の意味



Chart Co Jp



関数y Ax のグラフの性質 教遊者




中3数学 2次関数のグラフの特徴と練習問題



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



関数とは




関数y Ax2乗のグラフの書き方を教えてください ཀ Clearnote



中学数学 関数



関数y Ax のグラフの性質 教遊者




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




動画で学習 2 関数y Ax2のグラフ 数学




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート



Edu City Fukuyama Hiroshima Jp



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



Www1 Iwate School Jp



2次関数 グラフ 中学から数学だいすき




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット



Y Ax 2のグラフ Geogebra



1



4章 関数 Y Ax タカラゼミ




基礎数学のこの問題を教えてください Clearnote



至急 グラフの開き方が最も小さい関数は次のア オのどれですか また 開き方 Yahoo 知恵袋




二次関数y Ax2の放物線にみられる5つの特徴 Qikeru 学びを楽しくわかりやすく



Happylilac Net




課題をやれとは言ったが 答えを写せとは言ってねぇ 中間物語
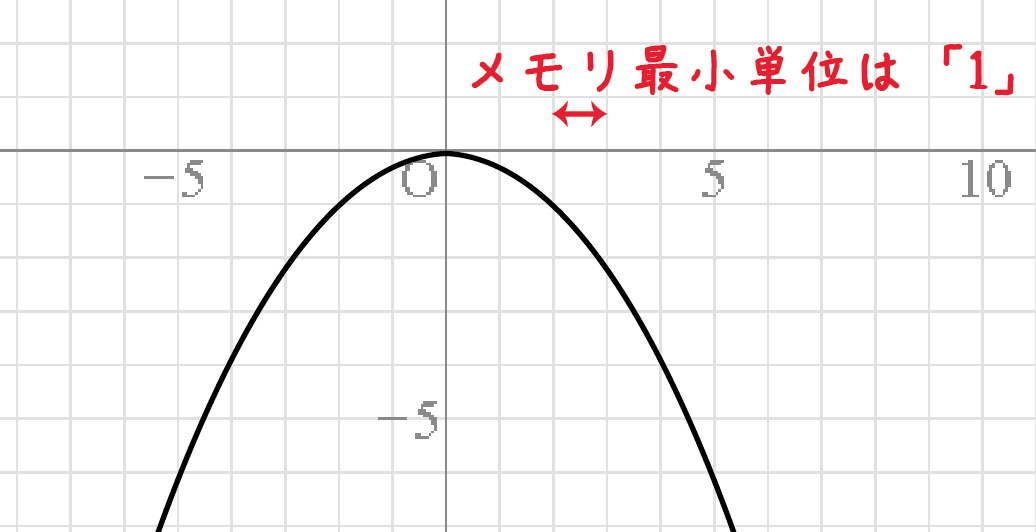



中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



何故y Ax のグラフはaの絶対値が大きいほど開き方が小さいのですか Yahoo 知恵袋
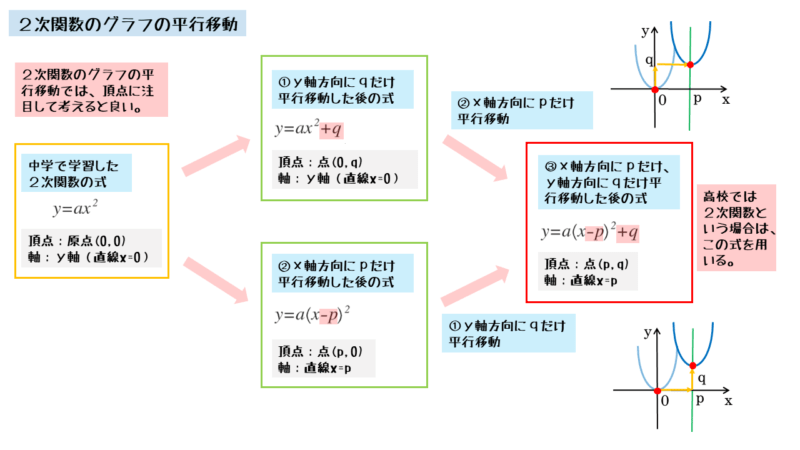



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん




課題をやれとは言ったが 答えを写せとは言ってねぇ 中間物語



Edu City Fukuyama Hiroshima Jp



Curricen2 Hokkaido C Ed Jp
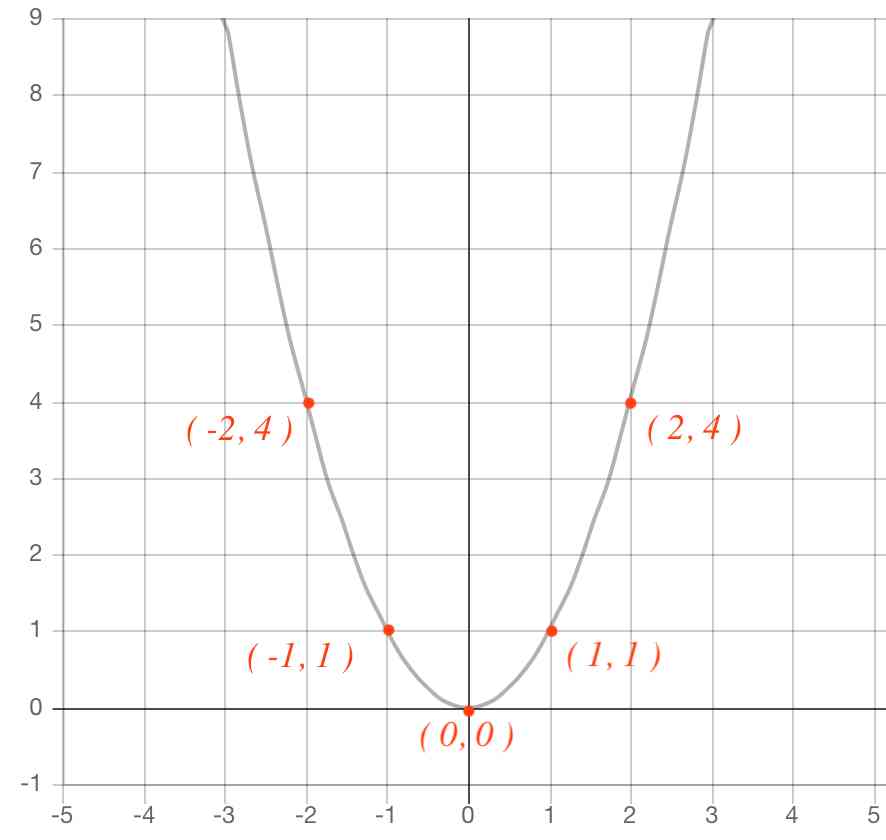



二次関数のグラフの書き方




例題で学ぶ高校数学 Y Ax2




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
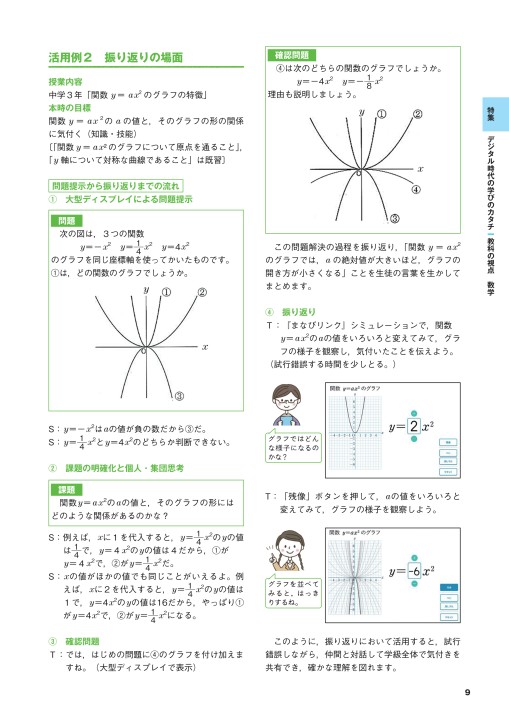



中学教科通信 21年5月号 ウェブ版



Edu City Fukuyama Hiroshima Jp




Y Ax2乗 グラフの特徴まとめ Youtube




2乗に比例する関数のグラフの特徴 無料で使える中学学習プリント



練成テキスト 必修編 数学
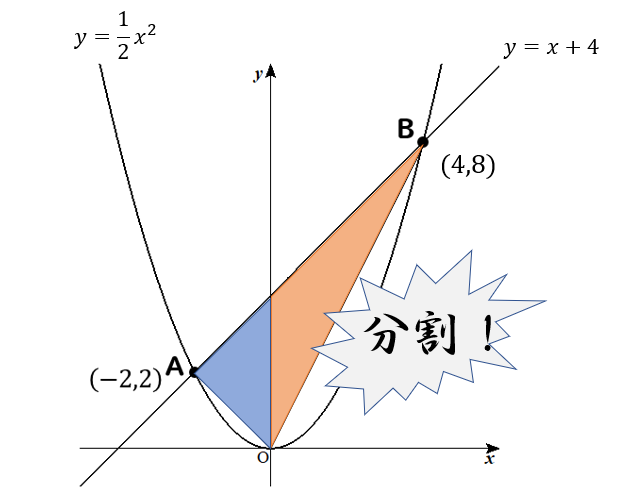



Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト




スタディピア 関数とグラフ




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく



二次関数とは 公式や 最大値 最小値 決定の問題の解き方 受験辞典




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



関数y Ax2について Aの値の絶対値が大きいだけ グラフの開きが小さ Yahoo 知恵袋




例題で学ぶ高校数学 Y Ax2
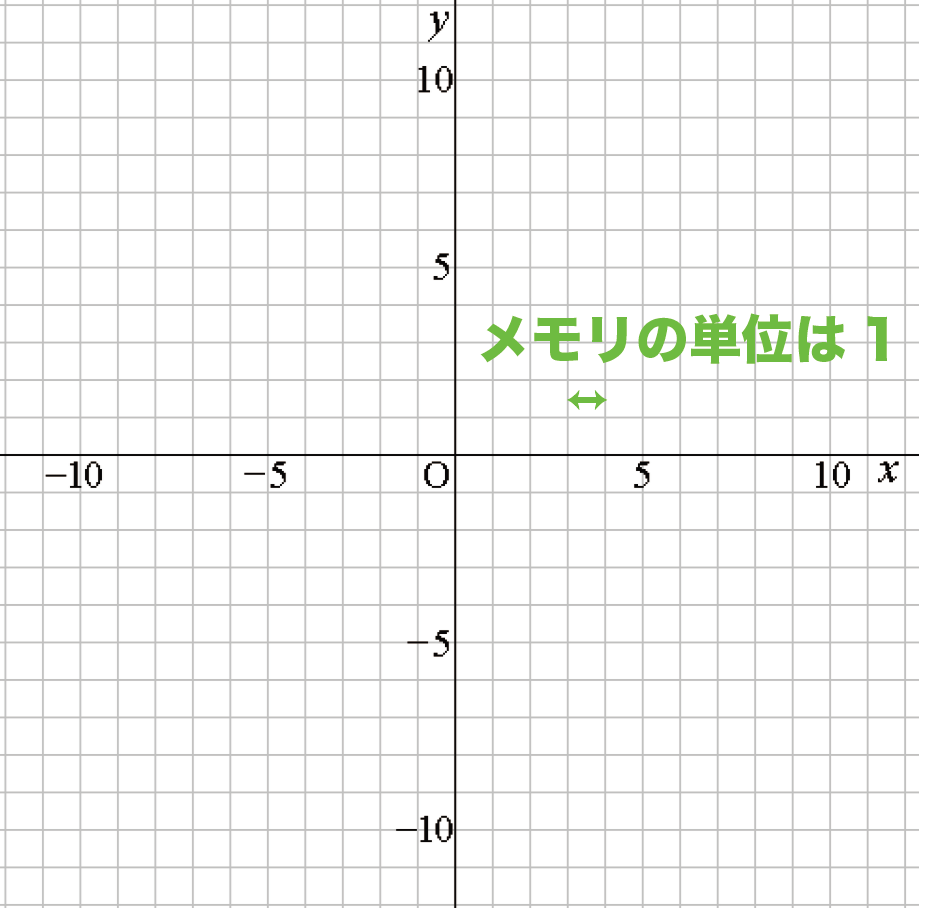



中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1
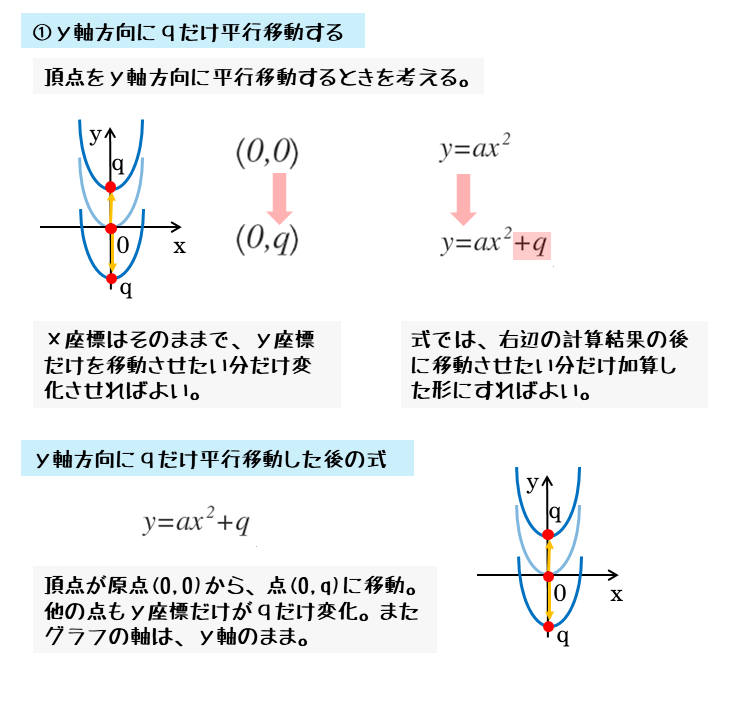



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん




スタディピア 関数とグラフ
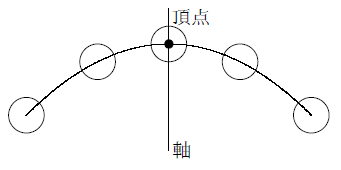



関数y Ax2のグラフ まなびの学園
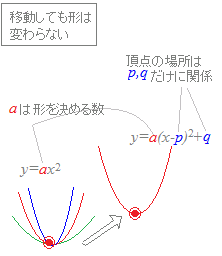



放物線の移動




スタディピア 関数とグラフ




Y Ax2 のグラフ



Rs Tottori U Ac Jp
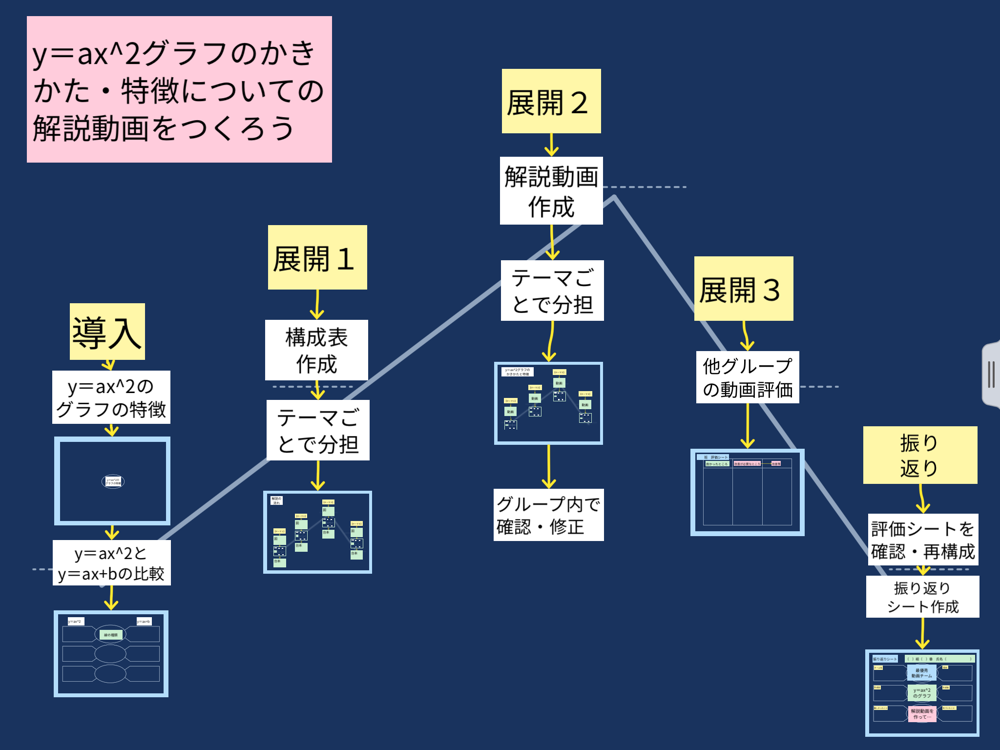



中3 算数 数学 関数 Y Ax 2グラフのかきかた 特徴について解説動画をつくろう 授業案 墨田区立桜堤中学校 岩井 洋平 ロイロノート スクール サポートページ



関数 中3




Y Ax2乗 変域の求め方 変域から式を作る方法について解説 中学数学 理科の学習まとめサイト



Chusuken Jp



Edu City Fukuyama Hiroshima Jp




中3 中3 数学 4章 関数y Ax 語句まとめ 中学生 数学のノート Clearnote
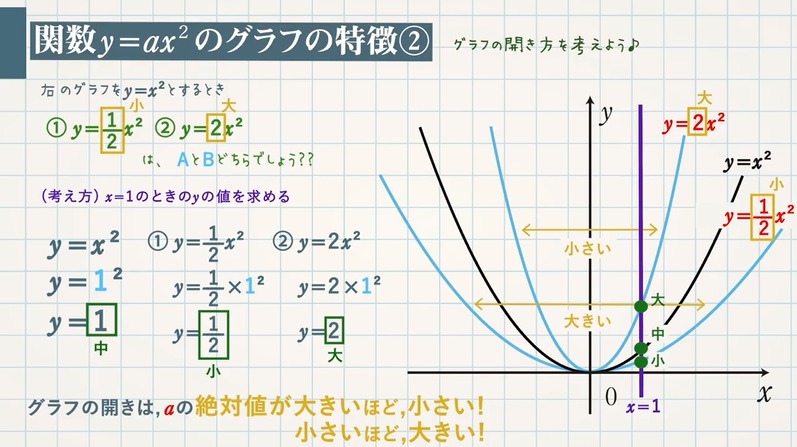



関数y Ax のグラフの性質 教遊者



2次関数の各係数の意味




数学 中3 35 二次関数のグラフ Youtube



1 2 2乗に比例する関数 2 グラフについて 工藤 謙



Cms Oklab Ed Jp
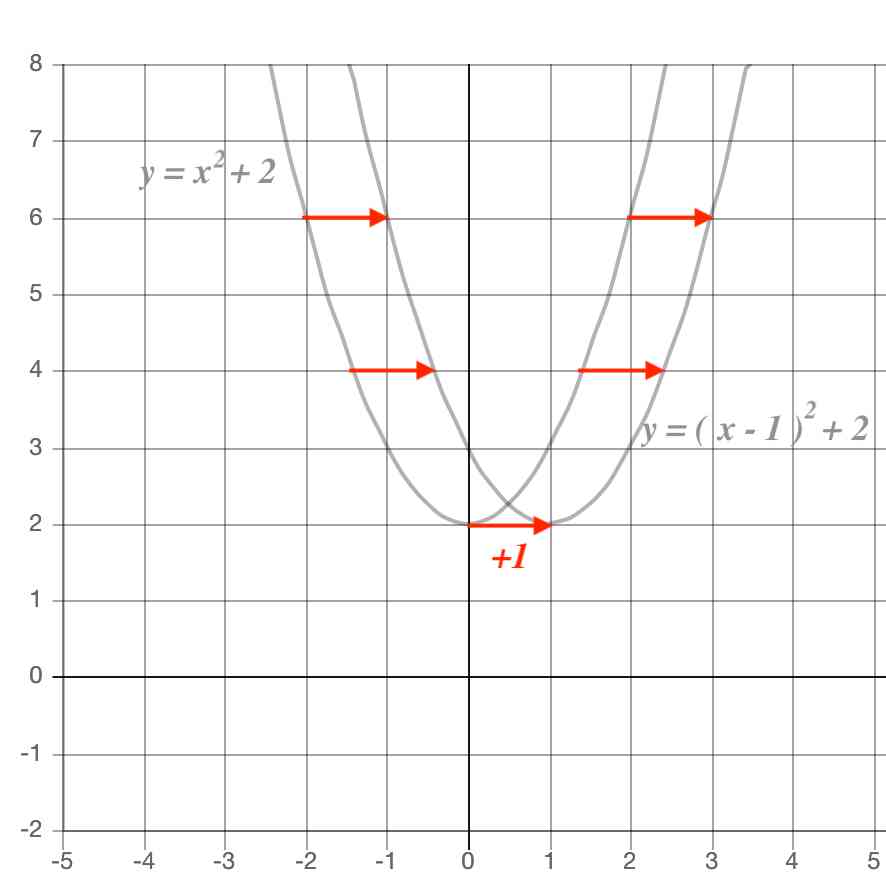



二次関数のグラフの書き方



辞書 二次関数のグラフの特徴 わかりmath
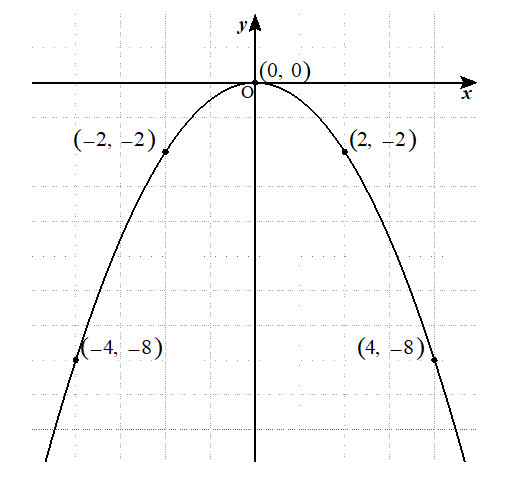



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ
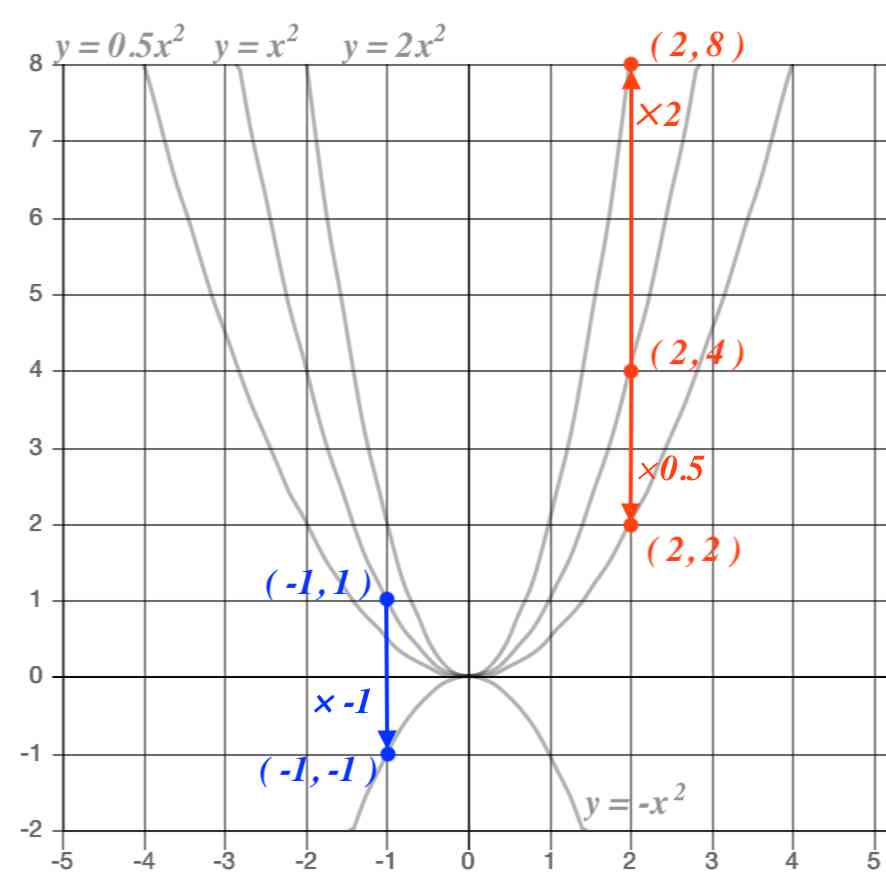



二次関数のグラフの書き方



Rs Tottori U Ac Jp




中3 関数y Ax二乗 基本 中学生 数学のノート Clearnote




Y Ax2乗 グラフの特徴まとめ Youtube



1



Ikushin Co Jp
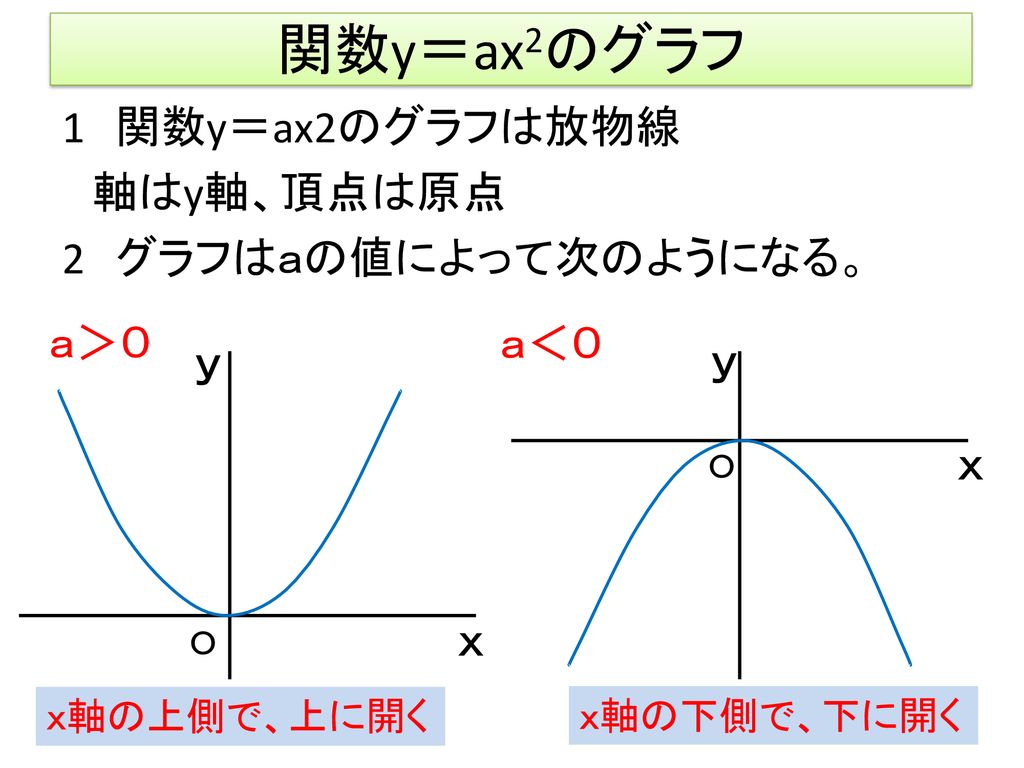



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download



Www1 Iwate School Jp



関数y Ax2乗のグラフ上に二点a Bがあり 点aの座標は 4 8 Yahoo 知恵袋




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト



辞書 二次関数のグラフの特徴 わかりmath




中3数学 Y Ax2乗の変域の求め方を解説 数スタ



2乗に比例する関数 グラフ



二次関数とは 公式や 最大値 最小値 決定の問題の解き方 受験辞典




Y Ax2乗 グラフの特徴と書き方をイチから解説します 中学数学 理科の学習まとめサイト
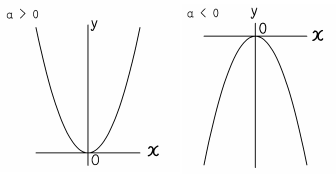



2乗に比例する関数 グラフ




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿